
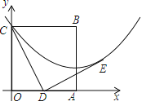
【题目】边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.点M为直线AB上一动点,点N为抛物线上一动点,当以点M,N,D,E为顶点的四边形是平行四边形时点N的坐标为___________.
【答案】(2,![]() )或(0,2)或(2,1)
)或(0,2)或(2,1)
【解析】
分三种情况讨论:N在抛物线顶点处;N在抛物线对称轴左侧;N在抛物线对称轴右侧.
解:∵AB为抛物线的对称轴,
∴设抛物线的解析式为![]() ,
,
∵正方形OABC边长为2
∴h=2,
∵![]() 经过C(0,2)和E两点,
经过C(0,2)和E两点,
过点E作EF⊥x轴于点F,如图1,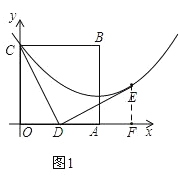
∵DE⊥DC,
∴∠CDO+∠EDF=90°,
∵∠CDO+∠OCD=90°,
∴∠OCD=∠EDF,
在△COD和△DFE中
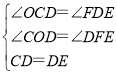
∴△COD≌△DFE(AAS),
∴OD=EF,DF=CO,
∵CO=OA=2,D为OA中点,
∴EF=OD=DA=1,DF=OC=2,
∴E(3,1);
∴C(0,2)和E(3,1)两点代入![]() ,
,
得:![]() ,解得:
,解得:![]()
∴抛物线的解析式为![]() ,
,
∴点N为抛物线上一动点,当以点M,N,D,E为顶点的四边形是平行四边形时点N的坐标可以分三种情况讨论:
(1) N在抛物线顶点处时,如图2所示,
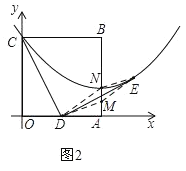
此时,N点就是抛物线的顶点(2,![]() );
);
(2)当N在抛物线对称轴左侧时,
过点C作CM∥DE交抛物线对称轴于点M,连接ME,如图3,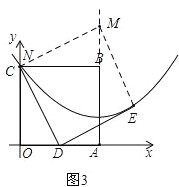
∵CM∥DE,DE⊥CD,
∴CM⊥CD,
∵OC⊥CB,
∴∠OCD=∠BCM,
在△OCD和△BCM中

∴△OCD≌△BCM(ASA),
∴CM=CD=DE,BM=OD=1,
∴CDEM是平行四边形,
即N点与C占重合,
∴N(0,2),
(3)N在抛物线对称轴右侧时,
N点在抛物线对称轴右侧,MN∥DE,如图4,
作NG⊥BA于点,延长DM交BN于点H,
∵MNED是平行四边形,
∴∠MDE=MNE,∠ENH=∠DHB,
∵BN∥DF,
∴∠ADH=∠DHB=∠ENH,
∴∠MNB=∠EDF,
在△BMN和△FED中
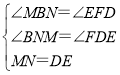
∴△BMN≌△FED(AAS),
∴BM=EF=1,
BN=DF=2,
∴M(2,1),
综上所述,点N的坐标为:(2,![]() )或(0,2)或(2,1)
)或(0,2)或(2,1)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=4,AD=3,E是边AB上一点(不与A. B重合),F是边BC上一点(不与B. C重合).若△DEF和△BEF是相似三角形,则CF的长度为( ).
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.
D.![]() 或1
或1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】原来公园有一个半径为 1 m 的苗圃,现在准备扩大面积,设当扩大后的半径为x m时,则增加的环形的面积为y m 2 .
(1)写出y与x的函数关系式;
(2)当半径增大到多少时面积增大1倍;
(3)试猜测半径是多少时,面积是原来的3、4、5、…倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(0,1)、B(3,3)、C(1,3).
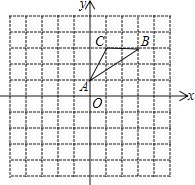
(1) 画出△ABC关于点O的中心对称图形△A1B1C1
(2) 画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为______.
(3) 若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9.
分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥x轴于B,且S△ABP=9.
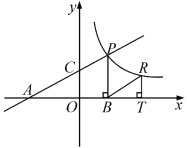
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥x轴于T,当△BRT与△AOC相似时,求点R的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(a+1)x2+2bx+(a+1)=0有两个相等的实数根,下列判断正确的是( )
A. 1一定不是关于x的方程x2+bx+a=0的根
B. 0一定不是关于x的方程x2+bx+a=0的根
C. 1和﹣1都是关于x的方程x2+bx+a=0的根
D. 1和﹣1不都是关于x的方程x2+bx+a=0的根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() 两点(
两点(![]() 在
在![]() 的左侧),直线
的左侧),直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .点
.点![]() 是
是![]() 轴上方的抛物线上一动点,过点
轴上方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ..
..
(1)求抛物线与x轴的交点坐标;
(2)设点![]() 的横坐标为
的横坐标为![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).
其中正确的结论有( )
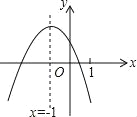
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD中,AE平分![]() 交BC于E,
交BC于E,![]() ,则下面的结论:①
,则下面的结论:①![]() 是等边三角形;②
是等边三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论有( )
,其中正确结论有( )
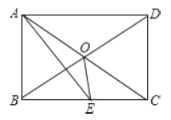
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com