Question

【题目】二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c＞0；（4）若点A（﹣3，y1）、点B（﹣ ，y2）、点C（ ，y3）在该函数图象上，则y1＜y3＜y2；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x1和x2 ， 且x1＜x2 ， 则x1＜﹣1＜5＜x2 ． 其中正确的结论有（　　）
A.2个
B.3个
C.4个
D.5个

Answer 1

【答案】B
【解析】解：（1）正确．∵﹣ =2， ∴4a+b=0．故正确．（2）错误．∵x=﹣3时，y＜0，
∴9a﹣3b+c＜0，
∴9a+c＜3b，故（2）错误．（3）正确．由图象可知抛物线经过（﹣1，0）和（5，0），
∴ 解得 ，
∴8a+7b+2c=8a﹣28a﹣10a=﹣30a，
∵a＜0，
∴8a+7b=2c＞0，故（3）正确．（4）错误，∵点A（﹣3，y1）、点B（﹣ ，y2）、点C（ ，y3），
∵ ﹣2= ，2﹣（﹣ ）= ，
∴ ＜
∴点C离对称轴的距离近，
∴y3＞y2 ，
∵a＜0，﹣3＜﹣ ＜2，
∴y1＜y2
∴y1＜y2＜y3 ， 故（4）错误．（5）正确．∵a＜0，
∴（x+1）（x﹣5）=﹣3/a＞0，
即（x+1）（x﹣5）＞0，
故x＜﹣1或x＞5，故（5）正确．
∴正确的有三个，
故选B．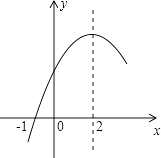

【考点精析】掌握二次函数图象以及系数a、b、c的关系是解答本题的根本，需要知道二次函数y=ax2+bx+c中，a、b、c的含义：a表示开口方向：a>0时，抛物线开口向上; a<0时，抛物线开口向下b与对称轴有关：对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标：（0，c）．