练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，周长为24的五边形ABCDE，被对角线BE分为等腰三角形ABE及矩形BCDE，且AB=BC．设AB长为x，CD为y，求y与x之间的函数关系，写出自变量的取值范围．
    考点：函数关系式,函数自变量的取值范围
    专题：
    分析：直接利用图形得出得出4x+2y=24，进而求出即可．
    解答：解：由题意可得：4x+2y=24，
    则y=-2x+12，
    由三角形三边关系得出：2x＞y，
    即2x＞-2x+12，
    解得：x＞3，
    4x＜24，
    解得：x＜6，
    故自变量的取值范围：3＜x＜6．
    点评：此题主要考查了函数关系式以及自变量取值范围求法，正确利用三角形三边关系得出是解题关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    设方程组
    ax2+bx+1=0
    bx2+x+a=0
    x2+ax+b=0
    有实数解，求a+b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：线段AB=a，M是AB的中点，C是AM的中点，D是CB的中点，求MD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一个邮递员骑自行车送信到某地，如果每小时行15km，就比预定时间少用24分钟；如果每小时行12km，就比预定时间多用15分钟，那么预定时间是多少小时？他去某地的路程是多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

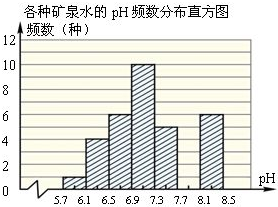    2008年 5月12日，我国四川省发生里氏8.0级地震，社会各界纷纷伸出援助之手捐钱捐物．根据国家质检总局的通知要求，对送往灾区食品、重要消费品必须进行检验检测，以确保运往灾区的食品等救灾物资的质量安全．如图是对某批数种矿泉水的抽查统计图，请观察图形，并回答下列问题：
    （1）被检查的矿泉水总数有多少种？
    （2）被检查的矿泉水的最低pH为多少？
    （3）组界为6.9～7.3这一组的频数、频率分别是多少？（每一组包括前一个边界值，不包括后一个边界值）
    （4）根据我过2001年公布的生活饮用水卫生规范，饮用水的pH应在6.5～8.5的范围内，被检测的矿泉水不符合这一标准的有多少种？占总数的百分之几？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

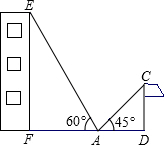    如图，在一次课外数学实践活动中，小明站在操场的A处，他的两侧分别是旗杆CD和一幢教学楼EF，点A、D、F在同一直线上，从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°，已知DF=16m，EF=18m，求旗杆CD高．（结果精确到0.1m，参考数据：
    		2
    ≈1.41，
    		3
    ≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知在⊙O中，直径AB=10cm，弦AC为6cm，∠ACB的平分线CD交⊙O于D，求BC、AD、BD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    任意两个三角形，△ABC和△A′B′C′，已知∠A=∠A′，∠B=∠B′，求证：△ABC∽△A′B′C′．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在平面直角坐标系中，A（18，0），B（12，8），C（0，8），动点P、Q分别从原点O、点B同时出发，动点P沿x轴正方向以每秒2个单位长度的速度运动，动点Q在线段BC上以每秒1的单位长度的速度向C运动，当点Q到达C点时，点P随之停止运动，设运动时间为t（秒），直线PQ与直线AB交于点D．
    （1）直接写出线段AB的长为
     
    ；
    （2）求直线AB的函数表达式；
    （3）当t=2时，求直线PQ的表达式以及点D的坐标；
    （4）直接写出所有t的值，使得此时△ADP是等腰三角形．

    查看答案和解析>>

    同步练习册答案