
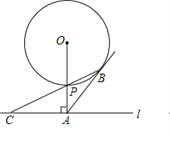
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5,OA与⊙O相交于点P,AB与⊙O相切于点B, BP的延长线交直线l于点C.
(1)试判断线段AB与AC的数量关系,并说明理由;
(2)若PC=![]() ,求⊙O的半径和线段PB的长;
,求⊙O的半径和线段PB的长;
(3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.

【答案】(1)AB=AC;理由见解析(2)⊙O的半径为3,线段PB的长为![]() ;(3)
;(3)![]() ≤r<5.
≤r<5.
【解析】试题分析:(1)连接OB,根据切线的性质和垂直得出∠OBA=∠OAC=90°,推出∠OBP+∠ABP=90°,∠ACP+∠CPA=90°,求出∠ACP=∠ABC,根据等腰三角形的判定推出即可;
(2)延长AP交⊙O于D,连接BD,设圆半径为r,则OP=OB=r,PA=5-r,根据AB=AC推出52-r2=(2![]() )2-(5-r)2,求出r,证△DPB∽△CPA,得出
)2-(5-r)2,求出r,证△DPB∽△CPA,得出![]() ,代入求出即可;
,代入求出即可;
(3)根据已知得出Q在AC的垂直平分线上,作出线段AC的垂直平分线MN,作OE⊥MN,求出OE<r,求出r范围,再根据相离得出r<5,即可得出答案.
试题解析:(1)AB=AC,理由如下:
连接OB.
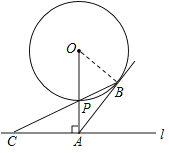
∵AB切⊙O于B,OA⊥AC,
∴∠OBA=∠OAC=90°,
∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,
∵OP=OB,
∴∠OBP=∠OPB,
∵∠OPB=∠APC,
∴∠ACP=∠ABC,
∴AB=AC;
(2)延长AP交⊙O于D,连接BD,
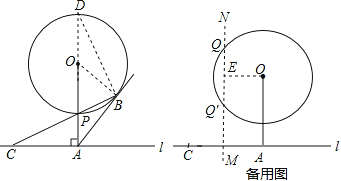
设圆半径为r,则OP=OB=r,PA=5-r,
则AB2=OA2-OB2=52-r2,
AC2=PC2-PA2=(2![]() )2-(5-r)2,
)2-(5-r)2,
∴52-r2=(2![]() )2-(5-r)2,
)2-(5-r)2,
解得:r=3,
∴AB=AC=4,
∵PD是直径,
∴∠PBD=90°=∠PAC,
又∵∠DPB=∠CPA,
∴△DPB∽△CPA,
∴![]() ,
,
∴![]() ,
,
解得:PB=![]() .
.
∴⊙O的半径为3,线段PB的长为![]() ;
;
(3)作出线段AC的垂直平分线MN,作OE⊥MN,则可以推出OE=![]() AC=
AC=![]() AB=
AB=![]()
又∵圆O与直线MN有交点,
∴OE=![]() ≤r,
≤r,
![]() ,
,
25-r2≤4r2,
r2≥5,
∴r≥![]() ,
,
又∵圆O与直线相离,
∴r<5,
即![]() ≤r<5.
≤r<5.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(-1,m)和点B(n,5).

(1)求该二次函数的关系式;
(2)在给定的平面直角坐标系中,画出这两个函数的大致图象;
(3)结合图象直接写出x2+bx+c>x+2时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
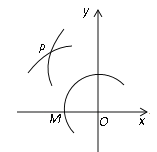
A. a=b B. 2a-b=1 C. 2a+b=-1 D. 2a+b=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在举行“弘扬中华传统文化读书月”活动结束后,对八年级(1)班40位学生所阅读书籍数量情况的统计结果如表所示:
阅读书籍数量(单位:本) | 1 | 2 | 3 | 3以上 |
人数(单位:人) | 12 | 16 | 9 | 3 |
这组数据的中位数和众数分别是( )
A. 2,2B. 1,2C. 3,2D. 2,1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com