
如图,△ABC中,AC=AD,BC=BE,∠ACB=100°,则∠ECD=( )
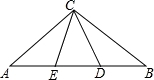
A.20° B.30° C.40° D.50°
C【考点】等腰三角形的性质.
【分析】首先设∠ACE=x°,∠DCE=y°,∠BCD=z°,由BE=BC,AD=AC,利用等腰三角形的性质,即可用x,y,z表示出∠ADC与∠BEC的度数,又由三角形外角的性质,得到∠A与∠B的值,然后由在△ABC中,∠ACB=100°,利用三角形内角和定理得到方程,继而求得∠DCE的大小.
【解答】解:设∠ACE=x°,∠DCE=y°,∠BCD=z°,
∵BE=BC,AD=AC,
∴∠ADC=∠ACD=∠ACE+∠DCE=(x+y)°,∠BEC=∠BCE=∠BCD+∠DCE=(y+z)°,
∴∠A=∠BEC﹣∠ACE=(y+z﹣x)°,∠B=∠ADC﹣∠BCD=(x+y﹣z)°,
∵在△ABC中,∠ACB=100°,
∴∠A+∠B=180°﹣∠ACB=80°,
∴y+z﹣x+x+y﹣z=80,
即2y=80,
∴y=40,
∴∠DCE=40°.
故选C.
【点评】本题考查了等腰三角形的性质、三角形内角和定理以及三角形外角的性质.此题难度适中,解答此题的关键是建立起各角之间的关系,结合图形列出方程进行解答.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
某商场销售的一款空调机每台的标价是1635元,在一次促销活动中,按标价的八折销售,仍可盈利9%.
(1)求这款空调每台的进价(利润率=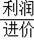
 =
=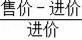
 ).
).
(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
下列计算正确的是( )
A.(﹣5b)3=﹣15b3 B.(2x)3(﹣5xy2)=﹣40x4y2
C.28x6y2+7x3y=4x2y D.(12a3﹣6a2+3a)÷3a=4a2﹣2a
查看答案和解析>>
科目:初中数学 来源: 题型:
已知两点P1(x1,y1)、P2(x2,y2)在函数y=
 的图象上,当x1>x2>0时,下列结论正确的是( )
的图象上,当x1>x2>0时,下列结论正确的是( )
A.0<y1<y2 B.0<y2<y1 C.y1<y2<0 D.y2<y1<0
查看答案和解析>>
科目:初中数学 来源: 题型:
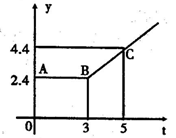
如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
(1)写出y与t之间的函数关系式;
(2)通话2分钟应付通话费多少元?通话7分钟呢?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com