
【题目】平面直角坐标系xOy中,横坐标为a的点A在反比例函数y1=![]() (x>0)的图象上,点B与点A关于原点O对称,一次函数y2=mx+n的图象经过点B.
(x>0)的图象上,点B与点A关于原点O对称,一次函数y2=mx+n的图象经过点B.
(1)设a=2,点C(4,2)在函数y1,y2的图象上.分别求函数y1,y2的表达式.
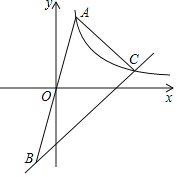
(2)如图,设函数y1,y2的图象相交于点C,点C的横坐标为3a,△ABC的面积为16,求k的值.
【答案】(1)y1=![]() ,y2=x﹣2;(2)k=6.
,y2=x﹣2;(2)k=6.
【解析】
(1)将点C(4,2)代入y1=![]() ,求出k的值,得到函数y1的表达式;把x=a=2代入y1=
,求出k的值,得到函数y1的表达式;把x=a=2代入y1=![]() ,求出点A坐标,根据A和点A'关于原点对称,得到点A'的坐标,将点A'和点B的坐标代入y2=mx+n,利用待定系数法求出函数y2的表达式;
,求出点A坐标,根据A和点A'关于原点对称,得到点A'的坐标,将点A'和点B的坐标代入y2=mx+n,利用待定系数法求出函数y2的表达式;
(2)由反比例函数图象上点的坐标特征可得点A坐标,根据A和点B关于原点对称,得到点B(﹣a,﹣![]() ).又点B在y2=mx+n的图象上,那么点B(﹣a,﹣am+n).解方程即可得到结论.
).又点B在y2=mx+n的图象上,那么点B(﹣a,﹣am+n).解方程即可得到结论.
解:(1)∵点C(4,2)在函数y1=![]() (x>0)的图象上,
(x>0)的图象上,
∴k=4×2=8,
∴函数y1的表达式为y1=![]() .
.
∵点A在y1=![]() 的图象上,
的图象上,
∴x=a=2,y=4,
∴点A(2,4).
∵A和点B关于原点对称,
∴点B的坐标为(﹣2,﹣4).
∵一次函数y2=mx+n的图象经过点A'和点B,
∴![]() ,
,
解之,得:![]() ,
,
∴函数y2的表达式为y2=x﹣2;
(2)∵点A的横坐标为a,
∴点A(a,![]() ).
).
∵A和点B关于原点对称,
∴点B的坐标为(﹣a,﹣![]() ).
).
∵点B在y2=mx+n的图象上,
∴点B的坐标为(﹣a,﹣am+n).
∴﹣![]() =﹣am+n,
=﹣am+n,
a2m=an+k①.
∵点C的横坐标为3a,
∴点C(3a,3am+n)或(3a,![]() ),
),
∴3am+n=![]() ,即9a2m+3an=k②
,即9a2m+3an=k②
由①②得:a2m=![]() ,an=﹣
,an=﹣![]() .
.
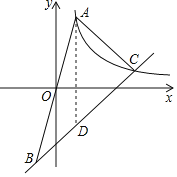
过点A作AD⊥x轴,交BC于点D,则点D(a,am+n),
∴AD=![]() ﹣am﹣n.
﹣am﹣n.
∵S△ABc=![]() AD(xc﹣xb)=
AD(xc﹣xb)=![]() 4a(
4a(![]() ﹣am﹣n)=16,
﹣am﹣n)=16,
∴k﹣a2m﹣an=8,
∴k﹣![]() ﹣(﹣
﹣(﹣![]() )=8,
)=8,
∴k=6.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点A在以BC为直径的半圆内.仅用 (不能使用圆规)分别按下列要求画图(保留画图痕迹).
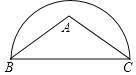
(1)请在图中画出BA边上的高CD;
(2)请在图中画出弦DE,使得DE∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教科书中这样写道:“我们把多项式![]() 及
及![]() 叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项使式子中出现完全平方式,再减去这个项,使整个式子的值不变这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求化数式最大值.最小值等.
例如:分解因式
![]() ;例如求代数式
;例如求代数式![]() 的最小值.
的最小值.![]() .可知当
.可知当![]() 时,
时,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根据阅读材料用配方法解决下列问题:
,根据阅读材料用配方法解决下列问题:
(1)分解因式:![]() _____
_____
(2)当![]() 为何值时,多项式
为何值时,多项式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
(3)当![]() 为何值时.多项式
为何值时.多项式![]() 有最小值并求出这个最小值
有最小值并求出这个最小值
查看答案和解析>>
科目:初中数学 来源: 题型:
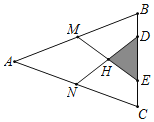
【题目】在△ABC中,AB=AC=13cm,BC=10cm,M、N分别是AB、AC的中点,D、E在BC上,且DE=5cm,连结DN、ME交于H,则△HDE的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象如图所示,以下结论:①abc>0; ②b2-4ac<0 ; ③2a+b>0 ;④a+b+c>0,其中正确的个数( )
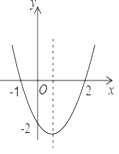
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP交CE于点D,∠CBP的平分线交CE于点Q,当CQ=QE时,EP+BP的值为( ).
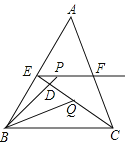
A.6B.9C.12D.18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小水池旁有一盏路灯,已知支架AB的长是0.8m,A端到地面的距离AC是4m,支架AB与灯柱AC的夹角为65°.小明在水池的外沿D测得支架B端的仰角是45°,在水池的内沿E测得支架A端的仰角是50°(点C、E、D在同一直线上),求小水池的宽DE.(结果精确到0.1m)(sin65°≈0.9,cos65°≈0.4,tan50°≈1.2)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图正方形ABCD的边长为2,点E,F,G,H分别在AD,AB,BC,CD上,且EA=FB=GC=HD,分别将△AEF,△BFG,△CGH,△DHE沿EF,FG,GH,HE翻折,得四边形MNKP,设AE=x(0<x<1),S四边形MNKP=y,则y关于x的函数图象大致为( )
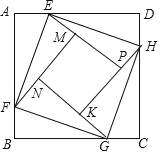
A. 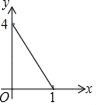 B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com