

分析 (1)由A(0,4),B(4,0),得到OA=OB=4,根据三角形的面积公式即可得到结论;
(2)过M作MD∥X轴交AB于D,根据平行线的性质得到∠MDC=∠NBC,∠DMC=∠BNC,通过△AMD是等腰直角三角形,得到AM=MD,等量代换得到MD=BN,推出△CAM≌△CNB(ASA),根据全等三角形的性质即可得到结论;
(3)过M作MF⊥Y轴交AB的延长线于F,则MF∥X轴,根据平行线的性质得到∠BNC=∠FMC,∠NBC=∠F,根据△AMF是等腰直角三角形,得到AM=MF,等量代换得到MF=BN,推出△BNC≌△FMC,根据全等三角形的性质得到结论.
解答 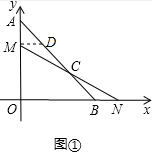 解:(1)∵A(0,4),B(4,0),
解:(1)∵A(0,4),B(4,0),
∴OA=OB=4,
∴S△OAB=$\frac{1}{2}$•OA•OB=8;
(2)如图①,过M作MD∥X轴交AB于D,
∴∠MDC=∠NBC,∠DMC=∠BNC,
∵∠OAB=45°,
∴△AMD是等腰直角三角形,
∴AM=MD,
∵AM=BN,
∴MD=BN,
在△CAM与△CNB中,$\left\{\begin{array}{l}{∠MDC=∠CBN}\\{∠DMC=∠CNB}\\{MD=BN}\end{array}\right.$,
∴△CAM≌△CNB(ASA),
∴CM=CN;
(3)CM=CN成立;
理由:如图②,过M作MF⊥Y轴交AB的延长线于F,则MF∥X轴,
∴∠BNC=∠FMC,∠NBC=∠F,
∵∠OAB=45°,
∴△AMF是等腰直角三角形,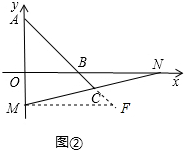
∴AM=MF,
∵AM=BN,
∴MF=BN,
在△BNC与△FMC中,$\left\{\begin{array}{l}{∠BNC=∠FMC}\\{∠NBC=∠F}\\{MF=BN}\end{array}\right.$,
∴△BNC≌△FMC,
∴CM=CN.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,坐标与图形的性质,正确的作出辅助线构造全等三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
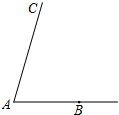 如图,已知∠CAB,用直尺和圆规作∠ABD,使∠ABD=$\frac{1}{2}$∠A,射线BD与射线AC相交于点D.(不写画法,保留作图痕迹)
如图,已知∠CAB,用直尺和圆规作∠ABD,使∠ABD=$\frac{1}{2}$∠A,射线BD与射线AC相交于点D.(不写画法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
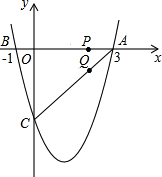 如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.
如图,二次函数y=$\frac{4}{3}$x2+bx+c的图象与x轴交于A(3,0),B(-1,0),与y轴交于点C.若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
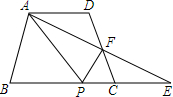 如图,在四边形ABCD中,AD∥BC,延长BC至点E,使CE=AD,连接AE交CD于点F,过点F作AE的垂线交BC于点P,连接PA.
如图,在四边形ABCD中,AD∥BC,延长BC至点E,使CE=AD,连接AE交CD于点F,过点F作AE的垂线交BC于点P,连接PA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
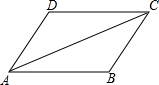 用2根同样长的木条AB,CD和另外两根同样长的木条AD,BC拼成一个四边形ABCD,
用2根同样长的木条AB,CD和另外两根同样长的木条AD,BC拼成一个四边形ABCD,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
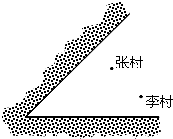 近年来,江苏省实施“村村通”工程和农村医疗卫生改革,宜兴市计划在某镇的张村、李村之间建一座定点医疗站P,张、李两村坐落在两相交公路内(如图所示),医疗站必须满足下列条件:①使其到两公路的距离相等;②到张、李两村的距离也相等.请你利用尺规作图确定P点的位置.(不写作法,保留作图痕迹)
近年来,江苏省实施“村村通”工程和农村医疗卫生改革,宜兴市计划在某镇的张村、李村之间建一座定点医疗站P,张、李两村坐落在两相交公路内(如图所示),医疗站必须满足下列条件:①使其到两公路的距离相等;②到张、李两村的距离也相等.请你利用尺规作图确定P点的位置.(不写作法,保留作图痕迹)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com