
【题目】阅读下列材料:
某同学遇到这样一个问题:在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 点
点![]() 在抛物线
在抛物线![]()
![]() 上,求点
上,求点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
如图1,他过点![]() 作
作![]() 于点
于点![]() 轴分别交
轴分别交![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() .他发现
.他发现![]()
![]() ,可求出
,可求出![]() 的长,再利用
的长,再利用![]() 求出
求出![]() 的长,即为点
的长,即为点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
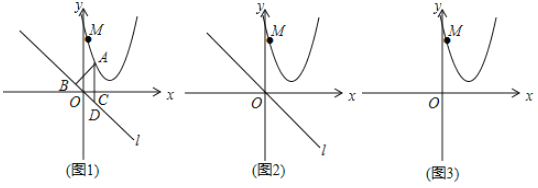
请回答:
(1)图1中,![]() ,点
,点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
参考该同学思考问题的方法,解决下列问题:
在平面直角坐标系![]() 中,点
中,点![]() 是抛物线
是抛物线![]() 上的一动点,设点
上的一动点,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(2)如图2,
①![]() ,则点
,则点![]() 的坐标为 ;
的坐标为 ;
②![]() ,在点
,在点![]() 运动的过程中,求
运动的过程中,求![]() 的最小值;
的最小值;
(3)如图3,![]() ,在点
,在点![]() 运动的过程中,
运动的过程中,![]() 的最小值是 .
的最小值是 .
【答案】(1)3,![]() ;(2)①(0,5)或(3,2);②
;(2)①(0,5)或(3,2);②![]() ;(3)
;(3)![]()
【解析】
(1)由题意得:d=AB=![]() AD=
AD=![]() ,即可求解;(2)如设点M的坐标为(m,m2-4m+5),则点N坐标为(m,-m),则由(1)知:d=MH=
,即可求解;(2)如设点M的坐标为(m,m2-4m+5),则点N坐标为(m,-m),则由(1)知:d=MH=![]() MN,即可求解;(3)如下图,点M的坐标为(m,m2-4m+5),则点N坐标为(m,2m-7),由题意得:tanα=2,则d=MH=MNcosα即可求解.
MN,即可求解;(3)如下图,点M的坐标为(m,m2-4m+5),则点N坐标为(m,2m-7),由题意得:tanα=2,则d=MH=MNcosα即可求解.
(1)∵点A(1,t)在抛物线y=x2-4x+5上,
∴t=1-4+5=2,
∴点A的坐标为(1,2).
∵AD∥y轴交直线l于点D,直线l:y=-x,
∴点D的坐标为(1,-1),
∴AD=2-(-1)=3.
∵△ABD为等腰直角三角形,∠ABD=90°,
∴d=AB=![]() AD=
AD=![]() .
.
(2)如图,过点M作y轴的平行线交直线l于点N,过点M作MH⊥l,交l于点H,设点M的坐标为(m,m2-4m+5),则点N坐标为(m,-m),则MN=m2-3m+5,
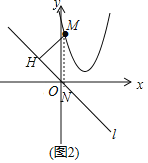 ,
,
∵![]() ,
,
∴![]() ,
,
解得:M坐标为(0,5)或(3,2);
②![]() ,
,
则d的最小值![]() ;
;
(3)如图,过点M作y轴的平行线交x轴于点G,交直线l于点N,过点M作MH⊥l,交l于点H,
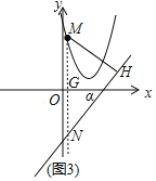
设点M的坐标为(m,m2-4m+5),则点N坐标为(m,2m-7),
由题意得:tanα=2,则![]() ,
,
则d=MH=MN![]() (m2-4m+5-2m+7)=
(m2-4m+5-2m+7)=![]() [(m-3)2+3],
[(m-3)2+3],
故d的最小值为![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=(x-m)2-(x-m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点.
(2)若该抛物线的对称轴为直线![]() ,求该抛物线的函数表达式.
,求该抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,老师提出了这样一个问题:如图,己知![]() .求作:过
.求作:过![]() 三点的圆.
三点的圆.
小芸是这样思考的:圆心确定一个圈的位置,半径确定一个圆的大小要作同时经过几个定点的圆,就是要先找到一个点,使得这个点到这几个定点的距离都相等.这样既定了圆心,又定了半径,就能画出满足条件的圆了.
小智听了小芸的分析后,按照这个思路很快就画出了一个过![]() 三点的圆.
三点的圆.
请你在答题纸上而出这个圆,并写出作图的主要依据,

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某养殖场在养殖面积扩建中,准备将总长为![]() 米的篱笆围成 矩形
米的篱笆围成 矩形![]() 形状的鸡舍,其中
形状的鸡舍,其中![]() 一边利用现有的一段足够长的围墙,其余三边 用篱笆,且在与墙平行的一边
一边利用现有的一段足够长的围墙,其余三边 用篱笆,且在与墙平行的一边![]() 上开一个
上开一个![]() 米宽的门
米宽的门![]() .设
.设![]() 边长为
边长为![]() 米, 鸡舍面积为
米, 鸡舍面积为![]() 平方米.
平方米.
![]() 求出
求出![]() 与
与![]() 的函数关系式;(不需写自变量的取值范围).
的函数关系式;(不需写自变量的取值范围).
![]() 当鸡舍的面积为
当鸡舍的面积为![]() 平方米时,求出鸡舍的一边
平方米时,求出鸡舍的一边![]() 的长.
的长.
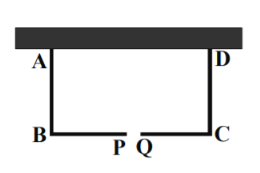
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 为等腰三角形,
为等腰三角形,![]() 是底边
是底边![]() 的中点,腰
的中点,腰![]() 与
与![]() 相切于点
相切于点![]() ,底
,底![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
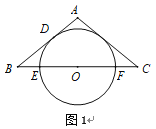
(1)求证:![]() 是
是![]() 的切线;
的切线;
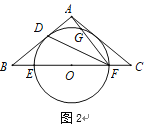
(2)如图2,连接![]() ,
,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 是弧
是弧![]() 的中点,若
的中点,若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com