
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是边AB上的高.
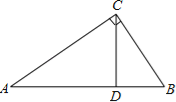
(1)求证:△ABC∽△CBD;
(2)如果AC=4,BC=3,求BD的长.
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)中的x和y满足下表:
x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 3 | 0 | -1 | 0 | m | 8 | … |
(1)可求得m的值为________;
(2)在坐标系画出该函数的图象;
(3)当y≥0时,x的取值范围为_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
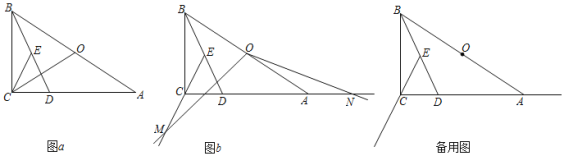
【题目】在Rt△ABC中,∠BCA=90°,∠A<∠ABC,D是AC边上一点,且DA=DB,O是AB的中点,CE是△BCD的中线.
(1)如图a,连接OC,请直接写出∠OCE和∠OAC的数量关系: ;
(2)点M是射线EC上的一个动点,将射线OM绕点O逆时针旋转得射线ON,使∠MON=∠ADB,ON与射线CA交于点N.
①如图b,猜想并证明线段OM和线段ON之间的数量关系;
②若∠BAC=30°,BC=m,当∠AON=15°时,请直接写出线段ME的长度(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为备战奥运会,中国女排的姑娘们刻苦训练,为国争光,如图,已知排球场的长度 OD 为 18 米,位于球场中线处球网的高度 AB 为 2.43 米,一队员站在点 O 处发球,排球从点 O 的正上方 1.8 米的 C 点向正前方飞出,当排球运行至离点 O 的水平距离 OE 为 7 米时,到达最高点 G,建立如图所示的平面直角坐标系.
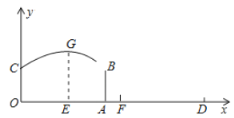
(1)当球上升的最大高度为 3.2 米时,求排球飞行的高度 y(单位:米)与水平距离 x(单位:米)的函数关系式.(不要求写出自变量 x 的取值范围)
(2)在(1)的条件下,对方距球网 0.5 米的点 F 处有一队员,她起跳后的最大高度为 3.1米,问这次她是否可以拦网成功?请通过计算说明.(不考虑排球的大小)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线型拱桥,当拱顶离水面![]() 时,水面宽
时,水面宽![]() 为
为![]() .当水面上升
.当水面上升![]() 时达到警戒水位,此时拱桥内的水面宽度是多少
时达到警戒水位,此时拱桥内的水面宽度是多少![]() ?
?
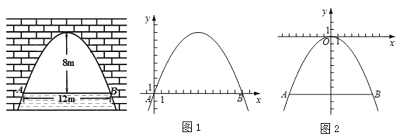
下面给出了解决这个问题的两种方法,请补充完整:
方法一:如图1.以点![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,此时点
,此时点![]() 的坐标为_______,抛物线的项点坐标为_______,可求这条抛物线所表示的二次函数解析式为_______.当
的坐标为_______,抛物线的项点坐标为_______,可求这条抛物线所表示的二次函数解析式为_______.当![]() 时,求出此时自变量
时,求出此时自变量![]() 的取值,即可解决这个问题.
的取值,即可解决这个问题.
方法二:如图2,以抛物线顶点为原点,对称轴为![]() 轴.建立平面直角坐标系
轴.建立平面直角坐标系![]() ,这时这条抛物线所表示的二次函数的解析式为_______,当水面达到警戒水位,即
,这时这条抛物线所表示的二次函数的解析式为_______,当水面达到警戒水位,即![]() _______时,求出此时自变量
_______时,求出此时自变量![]() 的取值为_______,从而得水面宽为
的取值为_______,从而得水面宽为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
某同学遇到这样一个问题:在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 点
点![]() 在抛物线
在抛物线![]()
![]() 上,求点
上,求点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
如图1,他过点![]() 作
作![]() 于点
于点![]() 轴分别交
轴分别交![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() .他发现
.他发现![]()
![]() ,可求出
,可求出![]() 的长,再利用
的长,再利用![]() 求出
求出![]() 的长,即为点
的长,即为点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
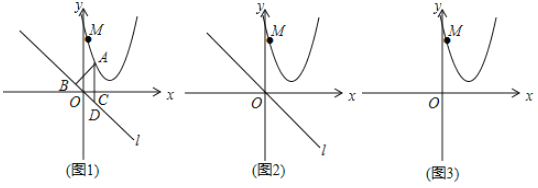
请回答:
(1)图1中,![]() ,点
,点![]() 到直线
到直线![]() 的距离
的距离![]() .
.
参考该同学思考问题的方法,解决下列问题:
在平面直角坐标系![]() 中,点
中,点![]() 是抛物线
是抛物线![]() 上的一动点,设点
上的一动点,设点![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(2)如图2,
①![]() ,则点
,则点![]() 的坐标为 ;
的坐标为 ;
②![]() ,在点
,在点![]() 运动的过程中,求
运动的过程中,求![]() 的最小值;
的最小值;
(3)如图3,![]() ,在点
,在点![]() 运动的过程中,
运动的过程中,![]() 的最小值是 .
的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、 点
、 点![]() 分别在线段
分别在线段![]() 和线段
和线段![]() 上,
上, ![]() 平分
平分![]() .
.
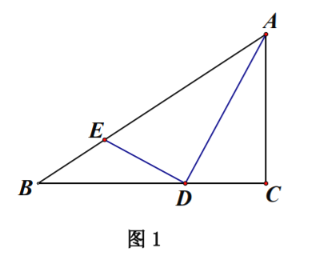
![]() 如图1,求证:
如图1,求证:![]() .
.
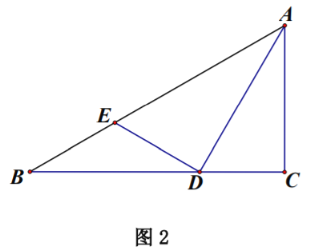
![]() 如图2,若
如图2,若![]() .求证:
.求证:![]() .
.
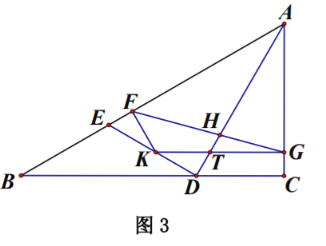
![]() 在
在![]() 问的条件下,如图3, 在线段
问的条件下,如图3, 在线段![]() 上取一点
上取一点![]() ,使
,使![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C,点C关于抛物线对称轴的对称点为点D,抛物线顶点为H(1,2).
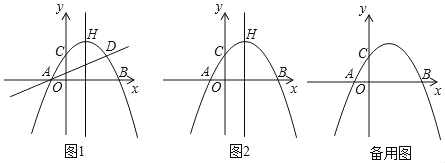
(1)求抛物线的解析式;
(2)点P为直线AD上方抛物线的对称轴上一动点,连接PA,PD.当S△PAD=3,若在x轴上存在一动点Q,使PQ+![]() QB最小,求此时点Q的坐标及PQ+
QB最小,求此时点Q的坐标及PQ+![]() QB的最小值;
QB的最小值;
(3)若点E为抛物线上的动点,点G,F为平面内的点,以BE为边构造以B,E,F,G为顶点的正方形,当顶点F或者G恰好落在y轴上时,求点E的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“分组合作学习”成为我市推动课堂教学改革,打造自主高效课堂的重要举措.某中学从全校学生中随机抽取100人作为样本,对“分组合作学习”实施前后学生的学习兴趣变化情况进行调查分析,统计如下:
分组前学生学习兴趣 分组后学生学习兴趣
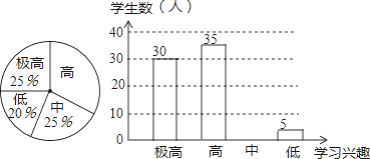
请结合图中信息解答下列问题:
(1)求出分组前学生学习兴趣为“高”的所占的百分比为 ;
(2)补全分组后学生学习兴趣的统计图;
(3)通过“分组合作学习”前后对比,请你估计全校2000名学生中学习兴趣获得提高的学生有多少人?请根据你的估计情况谈谈对“分组合作学习”这项举措的看法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com