
 如图,已知C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形有3对,它们分别是△ACD与△BCE;△ACF与△BCG;△GEC与△FDC.
如图,已知C是线段BD上一点,分别以BC,CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形有3对,它们分别是△ACD与△BCE;△ACF与△BCG;△GEC与△FDC. 分析 如图,分别证明△ACD≌△BCE、△ACF≌△BCG、△GEC≌△FDC,即可解决问题.
解答  解:如图,∵△ABC和△CDE均为等边三角形,
解:如图,∵△ABC和△CDE均为等边三角形,
∴∠ACB=∠ECD=60°,AC=BC,CE=CD,
∴∠BCE=∠ACD,∠ACE=180°-120°=60°;
在△ACD与△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴∠CAF=∠CBG,∠CEG=∠CDF;
在△ACF与△BCG中,
$\left\{\begin{array}{l}{∠CAF=∠CBG}\\{AC=BC}\\{∠ACF=∠BCG}\end{array}\right.$,
∴△ACF≌△BCG(ASA),
同理可证△GEC≌△FDC,
∴以点C为旋转中心,可通过旋转而相互得到的三角形有:△ACD与△BCE、△ACF与△BCG、△GEC与△FDC,共三对.
故答案为:△ACD与△BCE、△ACF与△BCG、△GEC与△FDC.
点评 该题主要考查了旋转变换的性质、全等三角形的判定及其性质等几何知识点的应用问题;深入观察图形,准确找出图形中隐含的相等或全等关系是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
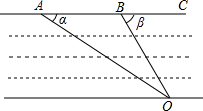 如图,要测量一段两岸平行的河的宽度,在A点测得∠α=30°,在B点测得∠β=60°,且AB=50米,则这段河岸的宽度为25$\sqrt{3}$米.
如图,要测量一段两岸平行的河的宽度,在A点测得∠α=30°,在B点测得∠β=60°,且AB=50米,则这段河岸的宽度为25$\sqrt{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
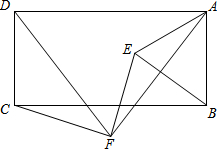 如图:F是矩形ABCD下方一点,将△FCD绕F点顺时针旋转60°后,恰好D点与A点重合,得到△FEA,连结EB得到△ABE,猜想并证明△ABE的形状.
如图:F是矩形ABCD下方一点,将△FCD绕F点顺时针旋转60°后,恰好D点与A点重合,得到△FEA,连结EB得到△ABE,猜想并证明△ABE的形状.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com