
【题目】如图,AB是半圆O的直径,过点O作弦AD的垂线交切线AC于点C,OC与圆O交于点E,连结BE、DE.
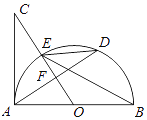
(1)若圆的半径是3,∠EBA是30度,求AD的长度.
(2)求证:∠BED=∠C.
(3)若OA=5,AD=8,求切线AC的长.
【答案】(1)AD=3![]() ;(2)证明见解析;(3)AC=
;(2)证明见解析;(3)AC=![]()
【解析】试题分析:(1)由垂径定理可得AF=DF,要求AD的长度,即要求AF的长度,由∠EBA=30°可以得出∠FOA=60°,进而得出∠FAO=30°,已知OA的长度结合30°余弦值,不难求出AF的长度,即可求出AD的长度;(2)要证∠BED=∠C即要证明∠DAB=∠C,由于∠C+∠CAF=90°,∠DAB+∠CAF=90°,不难证明;(3)连接BD,BD⊥AD,由勾股定理求出BD的长度,再由△OAC∽△BDA写出对应边的比值,即可求出AC的长度.
试题解析:
(1)解:∵∠EBA=30°,
∴∠AOF=60°,
∵OC⊥AD,
∴∠OAF=30°,AD=2AF,
∵AO=3,
∴AF=AO·cos30°=3×![]() =
=![]() ,
,
∴AD=2AF=3![]() ;
;
(2)
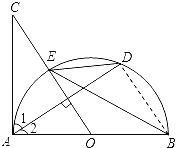
∵AC是⊙O的切线,AB是⊙O直径,
∴AB⊥AC.
∴∠1+∠2=90°,
∵OC⊥AD,
∴∠1+∠C=90°,
∴∠C=∠2,
∵∠BED=∠2,
∴∠BED=∠C;
(3)解:连接BD,
∵AB是⊙O直径,
∴∠ADB=90°,
∴BD=![]() =6,
=6,
∴△OAC∽△BDA,
∴OA∶BD=AC∶DA,
即5:6=AC:8,
∴AC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶A,B,C在小正方形的顶点上,利用网格作图:
(1)将△ABC水平向右平移4个单位得到△A1B1C1,画出△A1B1C1.
(2)过AB的中点D作DE∥BC交AC于点E;
(3)求出△ABC 的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家商铺进行维修,若请甲、乙两名工人同时施工,![]() 天可以完成,共需支付两人工资
天可以完成,共需支付两人工资![]() 元,若先请甲工人单独做
元,若先请甲工人单独做![]() 天,再请乙工人单独做
天,再请乙工人单独做![]() 天也可完成,共需付给两人工资
天也可完成,共需付给两人工资![]() 元
元
![]() 甲、乙工人单独工作一天,商铺应分别支付多少工资?
甲、乙工人单独工作一天,商铺应分别支付多少工资?
![]() 单独请哪名工人完成,商铺支付维修费用较少?
单独请哪名工人完成,商铺支付维修费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科学技术的发展,机器人早已能按照设计的指令完成各种动作.在坐标平面上,根据指令[S,α](S≥0,0°<α<180°)机器人能完成下列动作:先原地顺时针旋转角度α,再朝其对面方向沿直线行走距离s.
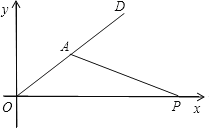
(1)填空:如图,若机器人在直角坐标系的原点,且面对y轴的正方向,现要使其移动到点A(2,2),则给机器人发出的指令应是 ;
(2)机器人在完成上述指令后,发现在P(6,0)处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能截住小球.
(参考数据:sin53°≈0.8,cos37°≈0.80,tan37°≈0.75,tan26.5°≈0.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分12分)如图,平行四边形OBCD中,OB=8cm,BC=6cm,∠DOB=45°,点P从O沿OB边向点B移动,点Q从点B沿BC边向点C移动,P,Q同时出发,速度都是1cm/s.
(1)求经过O,B,D三点的抛物线的解析式;
(2)判断P,Q移动几秒时,△PBQ为等腰三角形;
(3)若允许P点越过B点在BC上运动,Q点越过C点在CD上运动,设线PQ与OB,BC,DC围成的图形面积为y(cm2),点P,Q的移动时间为t(s),请写出y与t之间的函数关系式,并写出t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
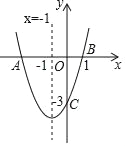
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
(1)求证:AE为⊙O的切线;
(2)当BC=4,AC=6时,求⊙O的半径;
(3)在(2)的条件下,求线段BG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你一定知道乌鸦喝水的故事吧!一个紧口瓶中盛有一些水,乌鸦想喝,但是嘴够不着瓶中的水,于是乌鸦衔来一些小石子放入瓶中,瓶中水面的高度随石子的增多而上升,乌鸦喝到了水.但是还没解渴,瓶中水面就下降到乌鸦够不着的高度,乌鸦只好再去衔些石子放入瓶中,水面又上升,乌鸦终于喝足了水,哇哇地飞走了.如果设衔入瓶中石子的体积为![]() ,瓶中水面的高度为
,瓶中水面的高度为![]() ,下面能大致表示上面故事情节的图象是( )
,下面能大致表示上面故事情节的图象是( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列网格中的六边形![]() 是由一个边长为6的正方形剪去左上角一个边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.
是由一个边长为6的正方形剪去左上角一个边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.
(1)根据剪拼前后图形的面积关系求出拼成的正方形的边长为___________;
(2)如图甲,把六边形![]() 沿
沿![]() ,
,![]() 剪成①,②,③三个部分,请在图甲中画出将②,③与①拼成的正方形,然后标出②,③变动后的位置;
剪成①,②,③三个部分,请在图甲中画出将②,③与①拼成的正方形,然后标出②,③变动后的位置;

(3)在图乙中画出一种与图甲不同位置的两条剪裁线,并画出将此六边形剪拼成的正方形.(通过平移,旋转,翻折与图甲重合的方法不可以)


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com