
【题目】观察、猜想、探究:
在△ABC中,![]() .
.
(1)如图①,当![]() ,AD为∠BAC的角平分线时,求证:
,AD为∠BAC的角平分线时,求证:![]() ;
;
(2)如图②,当![]() ,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的
,AD为∠BAC的角平分线时,线段AB、AC、CD又有怎样的
数量关系?请写出你的猜想,并对你的猜想给予证明;
(3)如图③,当AD为△ABC的外角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想.



【答案】(1)见解析;(2 ) ![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】试题分析:(1)过D作DE⊥AB,交AB于点E,理由角平分线性质得到DE=DC,利用HL得到Rt△ACD≌Rt△AED,由全等三角形的对应边相等,对应角相等,得到AC=AE,∠ACB=∠AED,由∠ACB=2∠B,利用等量代换及外角性质得到一对角相等,利用等角对等边得到BE=DE=DC,由AB=BE+AE,等量代换即可得证;
(2)AB=CD+AC,理由为:在AB上截取AG=AC,如图2所示,由角平分线定义得到一对角相等,再由![]() ,利用SAS得到△ADG≌△ADC,接下来同(1)即可得证;
,利用SAS得到△ADG≌△ADC,接下来同(1)即可得证;
(3)AB=CDAC,理由为:在AF上截取AG=AC,如图3所示,同(2)即可得证.
试题解析:(1)过D作DE⊥AB,交AB于点E,如图1所示,
∵AD为∠BAC的平分线,DC⊥AC,DE⊥AB,
∴DE=DC,
在Rt△ACD和Rt△AED中,
AD=AD,DE=DC,
∴Rt△ACD≌Rt△AED(HL),
∴AC=AE,∠ACB=∠AED,
∵∠ACB=2∠B,
∴∠AED=2∠B,
又∵∠AED=∠B+∠EDB,
∴∠B=∠EDB,
∴BE=DE=DC,
则AB=BE+AE=CD+AC;
(2)AB=CD+AC,理由为:
在AB上截取AG=AC,如图2所示,
∵AD为∠BAC的平分线,
∴∠GAD=∠CAD,
∵在△ADG和△ADC中,
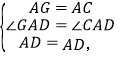
∴△ADG≌△ADC(SAS),
∴CD=DG,∠AGD=∠ACB,
∵∠ACB=2∠B,
∴∠AGD=2∠B,
又∵∠AGD=∠B+∠GDB,
∴∠B=∠GDB,
∴BE=DG=DC,
则AB=BG+AG=CD+AC;
(3)AB=CDAC,理由为:
在AF上截取AG=AC,如图3所示,
∵AD为∠FAC的平分线,
∴∠GAD=∠CAD,
∵在△ADG和△ACD中,
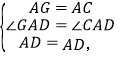
∴△ADG≌△ACD(SAS),
∴CD=GD,∠AGD=∠ACD,即∠ACB=∠FGD,
∵∠ACB=2∠B,
∴∠FGD=2∠B,
又∵∠FGD=∠B+∠GDB,
∴∠B=∠GDB,
∴BG=DG=DC,
则AB=BGAG=CDAC.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某学校为加强学生的体育锻炼,曾两次在某商场购买足球和篮球![]() 第一次购买6个足球和5个篮球共花费700元;第二次购买3个足球和7个篮球共花费710元.
第一次购买6个足球和5个篮球共花费700元;第二次购买3个足球和7个篮球共花费710元.
![]() 求足球和篮球的标价;
求足球和篮球的标价;
![]() 如果现在商场均以标价的6折对足球和篮球进行促销,学校决定从该商场再一次性购买足球和篮球60个,且总费用不能超过2500元,那么最多可以购买多少个篮球?
如果现在商场均以标价的6折对足球和篮球进行促销,学校决定从该商场再一次性购买足球和篮球60个,且总费用不能超过2500元,那么最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
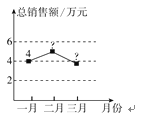
【题目】某运动品牌店对第一季度A,B两款运动鞋的销售情况进行统计,两款运动鞋的销售量及总销售额如图所示:
A,B两款运动鞋销售量统计图 A,B两款运动鞋总销售额统计图
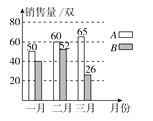
(1)一月份B款运动鞋的销售量是A款的![]() ,则一月份B款运动鞋销售了多少双?
,则一月份B款运动鞋销售了多少双?
(2)已知B款运动鞋500元/双,第一季度这两款运动鞋的销售单价保持不变,求二、三月份的总销售额(销售额=销售单价×销售量);
(3)结合第一季度的销售情况,请你对这两款运动鞋的进货、销售等方面提出一条建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】政府计划投资14万亿元实施东进战略.为了解民对东进战略的关注情况,佳佳随机采访部分民,并对采访情况制作了统计图表的一部分如下:
关注情况 | 频数 | 频率 |
A.高度关注 | m | 0.1 |
B.一般关注 | 200 | 0.5 |
C.不关注 | 60 | n |
D.不知道 | 100 | 0.25 |
(1)采访总人数为__ __人,m=__ __,n=__ __;
(2)补全统计图;
(3)估计在30 000名民中高度关注东进战略的人数约为 人.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上, 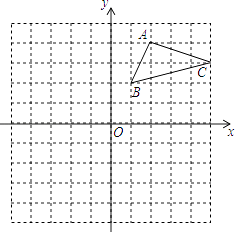
(1)画出△ABC关于x轴对称的△A1B1C1 .
(2)画出△ABC绕原点O旋转180°后的△A2B2C2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用棋子摆成的“上”字.
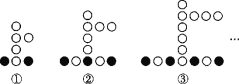
(1)依照此规律,第4个图形需要黑子、白子各多少枚?
(2)按照这样的规律摆下去,摆成第n个“上”字需要黑子、白子各多少枚?
(3)请探究第几个“上”字图形白子总数比黑子总数多15枚.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动,当一点到达终点时,另一点也停止运动.设运动时间为x秒,△PBQ的面积为y(cm2). 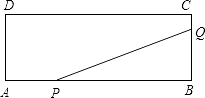
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,E是BC的中点,过点E作EF⊥AE,交CD于点F,连接AF并延长,交BC的延长线于点G.则CG的长为( ) 
A.![]()
B.1
C.![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 是Δ
是Δ![]() 的一个外角,我们容易证明
的一个外角,我们容易证明![]() =
=![]() ,即三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
,即三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
尝试探究:
(![]() )如图2,
)如图2,![]() 与
与![]() 分别为
分别为![]() 的两个外角,则
的两个外角,则![]()
![]() (横线上填 >、< 或=)
(横线上填 >、< 或=)
初步应用:
(![]() )如图3,在
)如图3,在![]() 纸片中剪去
纸片中剪去![]() ,得到四边形
,得到四边形![]() ,
,![]() ,则
,则![]() .
.
(![]() )解决问题:如图4,在
)解决问题:如图4,在![]() 中,
中,![]() 、
、![]() 分别平分外角
分别平分外角![]() 、
、![]() ,
,![]() 与
与![]() 有何数量关系?请利用上面的结论直接写出答案 .
有何数量关系?请利用上面的结论直接写出答案 .
(![]() )如图5,在四边形
)如图5,在四边形![]() 中,
中,![]() 、
、![]() 分别平分外角
分别平分外角![]() 、
、![]() ,请利用上面的结论探究
,请利用上面的结论探究![]() 与
与![]() 、
、![]() 的数量关系.
的数量关系.

图1 图2 图3

图4 图5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com