
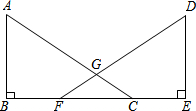
 已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE,求证:∠A=∠D.
已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=CE,求证:∠A=∠D. 科目:初中数学 来源: 题型:解答题
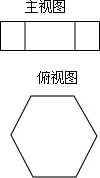 如图是一个直六棱柱的不完整的三视图,其中主视图是一个邻边为20和8的矩形,俯视图是正六边形
如图是一个直六棱柱的不完整的三视图,其中主视图是一个邻边为20和8的矩形,俯视图是正六边形查看答案和解析>>
科目:初中数学 来源: 题型:解答题
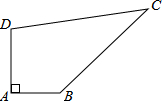 如图所示,学校内有一块四边形的空地ABCD,现计划在该空地上种植草坪经测量,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草坪皮需要400元,问需要投入多少元?
如图所示,学校内有一块四边形的空地ABCD,现计划在该空地上种植草坪经测量,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草坪皮需要400元,问需要投入多少元?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
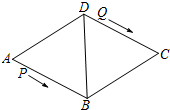 如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB-BD做匀速运动,动点Q从点D同时出发,沿着线路DC-CB-BA做匀速运动.
如图,菱形ABCD的边长为48cm,∠A=60°,动点P从点A出发,沿着线路AB-BD做匀速运动,动点Q从点D同时出发,沿着线路DC-CB-BA做匀速运动. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
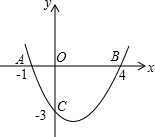 如图,已知二次函数y=ax2+bx+c的图象与x轴交于点A、B,与y轴交于点C.
如图,已知二次函数y=ax2+bx+c的图象与x轴交于点A、B,与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
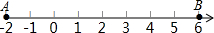 如图,数轴上A,B两点表示的数分别为-2和6,数轴上的点C是AB的中点,数轴上点D,使AD=$\frac{3}{2}$AC,则线段BD的长是2或14.
如图,数轴上A,B两点表示的数分别为-2和6,数轴上的点C是AB的中点,数轴上点D,使AD=$\frac{3}{2}$AC,则线段BD的长是2或14.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com