
【题目】如图,△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,DH⊥BC于H,交BE于G.下列结论:①BD=CD;②AD+CF=BD;③CE=![]() BF;④AE=BG.其中正确的是
BF;④AE=BG.其中正确的是

A. ①② B. ①③ C. ①②③ D. ①②③④
【答案】C
【解析】
根据∠ABC=45°,CD⊥AB可得出BD=CD,利用AAS判定Rt△DFB≌Rt△DAC,从而得出DF=AD,BF=AC.则CD=CF+AD,即AD+CF=BD;再利用AAS判定Rt△BEA≌Rt△BEC,得出CE=AE=![]() AC,又因为BF=AC所以CE=
AC,又因为BF=AC所以CE=![]() AC=
AC=![]() BF,连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG.在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.
BF,连接CG.因为△BCD是等腰直角三角形,即BD=CD.又因为DH⊥BC,那么DH垂直平分BC.即BG=CG.在Rt△CEG中,CG是斜边,CE是直角边,所以CE<CG.即AE<BG.
∵CD⊥AB,∠ABC=45°,
∴△BCD是等腰直角三角形.
∴BD=CD.故①正确;
在Rt△DFB和Rt△DAC中,
∵∠DBF=90°∠BFD,∠DCA=90°∠EFC,且∠BFD=∠EFC,
∴∠DBF=∠DCA.
又∵∠BDF=∠CDA=90°,BD=CD,
∴△DFB≌△DAC.
∴BF=AC;DF=AD.
∵CD=CF+DF,
∴AD+CF=BD;故②正确;
在Rt△BEA和Rt△BEC中.
∵BE平分∠ABC,
∴∠ABE=∠CBE.
又∵BE=BE,∠BEA=∠BEC=90°,
∴Rt△BEA≌Rt△BEC.
∴CE=AE=![]() AC.
AC.
又由(1),知BF=AC,
∴CE=![]() AC=
AC=![]() BF;故③正确;
BF;故③正确;
连接CG.

∵△BCD是等腰直角三角形,
∴BD=CD.
又DH⊥BC,
∴DH垂直平分BC.∴BG=CG.
在Rt△CEG中,
∵CG是斜边,CE是直角边,
∴CE<CG.
∵CE=AE,
∴AE<BG.故④错误.
故选C.


科目:初中数学 来源: 题型:
【题目】如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
(1)当a=10米时,花圃的面积=
(2)通道的面积与花圃的面积之比能否恰好等于3:5,如果可以,求出此时通道的宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
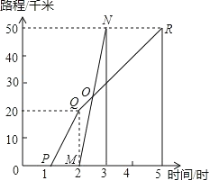
【题目】如图所示 A、B 两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按同路从A地出发驶往B地.如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S与该日下午时间t之间的关系.
(1)甲乙两人中, 先出发,先出发 小时.
(2)甲乙两人中, 先到达B地,先到 小时.
(3)分别求出乙骑摩托车的速度和甲骑自行车在全程的平均速度.
(4)乙出发大约用多长时间就追上甲?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示运动时间(0≤t≤6),那么当t为何值时,△APQ与△ABD相似?说明理由. 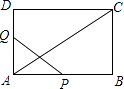
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC=25,AB=30,D是AB上的一点(不与A、B重合),DE⊥BC,垂足是点E,设BD=x,四边形ACED的周长为y,则下列图象能大致反映y与x之间的函数关系的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在正方形ABCD中,E是CD边上的一点,F为BC延长线上一点,且CE=CF.
(1)求证:△BEC≌△DFC;
(2)若正方形ABCD的面积16,CF=3,求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com