
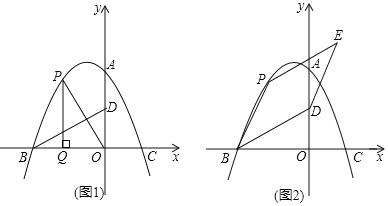
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨∂˛¥Œ∫Ø ˝y£Ω©Å![]() x2+bx+cµƒÕºœÛ”Îy÷·Ωª”⁄µ„A£®0£¨8£©£¨”Îx÷·Ωª”⁄B°¢C¡Ωµ„£¨∆‰÷–µ„Cµƒ◊¯±ÍŒ™£®4£¨0£©£Æµ„P£®m£¨n£©Œ™∏√∂˛¥Œ∫Ø ˝‘⁄µ⁄∂˛œÛœÞƒ⁄ÕºœÛ…œµƒ∂ص„£¨µ„Dµƒ◊¯±ÍŒ™£®0£¨4£©£¨¡¨Ω”BD£Æ
x2+bx+cµƒÕºœÛ”Îy÷·Ωª”⁄µ„A£®0£¨8£©£¨”Îx÷·Ωª”⁄B°¢C¡Ωµ„£¨∆‰÷–µ„Cµƒ◊¯±ÍŒ™£®4£¨0£©£Æµ„P£®m£¨n£©Œ™∏√∂˛¥Œ∫Ø ˝‘⁄µ⁄∂˛œÛœÞƒ⁄ÕºœÛ…œµƒ∂ص„£¨µ„Dµƒ◊¯±ÍŒ™£®0£¨4£©£¨¡¨Ω”BD£Æ
£®1£©«Û∏√∂˛¥Œ∫Ø ˝µƒ±Ì¥Ô Ωº∞µ„Bµƒ◊¯±Í£ª
£®2£©¡¨Ω”OP£¨π˝µ„P◊˜PQ°Õx÷·”⁄µ„Q£¨µ±“‘O°¢P°¢QŒ™∂•µ„µƒ»˝Ω«–Œ”ΰ˜OBDœýÀ∆ ±£¨«Ûmµƒ÷µ£ª
£®3£©¡¨Ω”BP£¨“‘BD°¢BPŒ™¡⁄±þ◊˜BDEP£¨÷±œþPEΩªx÷·”⁄µ„T£Æµ±µ„E¬‰‘⁄∏√∂˛¥Œ∫Ø ˝ÕºœÛ…œ ±£¨«Ûµ„Eµƒ◊¯±Í£Æ
°æ¥∞∏°ø£®1£©![]() ,£®©Å8£¨0£©£ª£®2£©©Å4ªÚ©Å1©Å
,£®©Å8£¨0£©£ª£®2£©©Å4ªÚ©Å1©Å![]() £ª£®3£©£®1£¨
£ª£®3£©£®1£¨![]() £©.
£©.
°æΩ‚Œˆ°ø
£®1£©÷±Ω”Ω´A£¨C¡Ωµ„¥˙»Îº¥ø…«Û
£®2£©ø……ËP£®m£¨-![]() m2-m+8£©£¨”…°œOQP=°œBOD=90°„£¨‘Ú∑÷¡Ω÷÷«Èøˆ£∫°˜POQ°◊°˜OBD∫Õ°˜POQ°◊°˜OBD∑÷±«Û≥ˆPQ”ÎOQµƒπÿœµº¥ø…
m2-m+8£©£¨”…°œOQP=°œBOD=90°„£¨‘Ú∑÷¡Ω÷÷«Èøˆ£∫°˜POQ°◊°˜OBD∫Õ°˜POQ°◊°˜OBD∑÷±«Û≥ˆPQ”ÎOQµƒπÿœµº¥ø…
£®3£©◊˜∆Ω––Àƒ±þ–Œ£¨ µ÷ «Ω´B°¢PœÚ”“∆Ω“∆8∏ˆµ•Œª£¨‘ŸœÚ…œ∆Ω“∆4∏ˆµ•Œªº¥ø…µ√µΩµ„E∫Õµ„D£¨µ„E‘⁄∂˛¥Œ∫Ø ˝…œ£¨¥˙»Îº¥ø…«Ûmµƒ÷µ£¨¥”∂¯«Ûµ√µ„Eµƒ◊¯±Í£Æ
£®1£©∞—A£®0£¨8£©£¨C£®4£¨0£©¥˙»Îy£Ω©Å![]() x2+bx+cµ√
x2+bx+cµ√
![]() £¨Ω‚µ√
£¨Ω‚µ√![]()
°ý∏√∂˛¥Œ∫Ø ˝µƒ±Ì¥ÔŒ™y£Ω©Å![]() x2©Åx+8
x2©Åx+8
µ±y£Ω0 ±£¨©Å![]() x2©Åx+8£Ω0£¨Ω‚µ√x1£Ω©Å8£¨x2£Ω4
x2©Åx+8£Ω0£¨Ω‚µ√x1£Ω©Å8£¨x2£Ω4
°ýµ„Bµƒ◊¯±ÍŒ™£®©Å8£¨0£©
£®2£©…ËP£®m£¨©Å![]() m2©Åm+8£©£¨”…°œOQP£Ω°œBOD£Ω90°„£¨∑÷¡Ω÷÷«Èøˆ£∫
m2©Åm+8£©£¨”…°œOQP£Ω°œBOD£Ω90°„£¨∑÷¡Ω÷÷«Èøˆ£∫
µ±°˜POQ°◊°˜OBD ±£¨![]()
°ýPQ£Ω2OQ
º¥©Å![]() m2©Åm+8£Ω2°¡£®©Åm£©£¨Ω‚µ√m£Ω©Å4£¨ªÚm£Ω8£®…·»•£©
m2©Åm+8£Ω2°¡£®©Åm£©£¨Ω‚µ√m£Ω©Å4£¨ªÚm£Ω8£®…·»•£©
µ±°˜POQ°◊°˜OBD ±£¨![]()
°ýOQ£Ω2PQ
º¥©Åm£Ω2°¡£®©Å![]() m2©Åm+8£©£¨Ω‚m£Ω©Å1©Å
m2©Åm+8£©£¨Ω‚m£Ω©Å1©Å![]() ªÚm£Ω©Å1+
ªÚm£Ω©Å1+![]() £®…·»•£©
£®…·»•£©
◊€…œÀ˘ ˆ£¨mµƒ÷µŒ™©Å4ªÚ©Å1©Å![]()
£®3£©°þÀƒ±þ–ŒBDEPŒ™∆Ω––Àƒ±þ–Œ£¨
°ýPE°ŒBD£¨PE£ΩBD
°þµ„BœÚ”“∆Ω“∆8∏ˆµ•Œª£¨‘ŸœÚ…œ∆Ω“∆4∏ˆµ•Œªµ√µΩµ„D
°ýµ„PœÚ”“∆Ω“∆8∏ˆµ•Œª£¨‘ŸœÚ…œ∆Ω∫‚4∏ˆµ•Œªµ√µΩµ„E
°þµ„P£®m£¨©Å![]() m2©Åm+8£©£¨
m2©Åm+8£©£¨
°ýµ„E£®m+8£¨©Å![]() m2©Åm+12£©£¨
m2©Åm+12£©£¨
°þµ„E¬‰‘⁄∂˛¥Œ∫Ø ˝µƒÕºœÛ…œ
°ý©Å![]() £®m+8£©2©Å£®m+8£©+8£Ω©Å
£®m+8£©2©Å£®m+8£©+8£Ω©Å![]() m2©Åm+12
m2©Åm+12
Ω‚µ√£¨m£Ω©Å7
°ýµ„Eµƒ◊¯±ÍŒ™£®1£¨![]() £©£Æ
£©£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™£∫»ÁÕº£¨∑¥±»¿˝∫Ø ˝![]() µƒÕºœÛ”Γª¥Œ∫Ø ˝
µƒÕºœÛ”Γª¥Œ∫Ø ˝![]() µƒÕºœÛΩª”⁄µ„
µƒÕºœÛΩª”⁄µ„![]() °¢µ„
°¢µ„![]() .
.
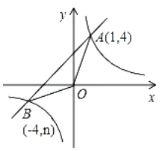
£®1£©«Û“ª¥Œ∫Ø ˝∫Õ∑¥±»¿˝∫Ø ˝µƒΩ‚Œˆ Ω£ª
£®2£©«Û![]() µƒ√ʪ˝£ª
µƒ√ʪ˝£ª
£®3£©÷±Ω”–¥≥ˆ“ª¥Œ∫Ø ˝÷µ¥Û”⁄∑¥±»¿˝∫Ø ˝÷µµƒ◊‘±‰¡ø![]() µƒ»°÷µ∑∂Œß.
µƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®1£©Œ Â∑¢œ÷
»ÁÕº1£¨‘⁄°˜OAB∫Õ°˜OCD÷–£¨OA=OB£¨OC=OD£¨°œAOB=°œCOD=40°„£¨¡¨Ω”AC£¨BDΩª”⁄µ„M£ÆÃÓø’£∫
¢Ÿ![]() µƒ÷µŒ™°° °°£ª
µƒ÷µŒ™°° °°£ª
¢⁄°œAMBµƒ∂» ˝Œ™°° °°£Æ
£®2£©¿ý±»ÃΩæø
»ÁÕº2£¨‘⁄°˜OAB∫Õ°˜OCD÷–£¨°œAOB=°œCOD=90°„£¨°œOAB=°œOCD=30°„£¨¡¨Ω”ACΩªBDµƒ—”≥§œþ”⁄µ„M£Æ«Î≈–∂œ![]() µƒ÷µº∞°œAMBµƒ∂» ˝£¨≤¢Àµ√˜¿Ì”…£ª
µƒ÷µº∞°œAMBµƒ∂» ˝£¨≤¢Àµ√˜¿Ì”…£ª
£®3£©Õÿ’π—”…Ï
‘⁄£®2£©µƒÃıº˛œ¬£¨Ω´°˜OCD»∆µ„O‘⁄∆Ω√ʃ⁄–˝◊™£¨AC£¨BDÀ˘‘⁄÷±œþΩª”⁄µ„M£¨»ÙOD=1£¨OB=![]() £¨«Î÷±Ω”–¥≥ˆµ±µ„C”ε„M÷ÿ∫œ ±ACµƒ≥§£Æ
£¨«Î÷±Ω”–¥≥ˆµ±µ„C”ε„M÷ÿ∫œ ±ACµƒ≥§£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®1£©‘ƒ∂¡¿ÌΩ‚
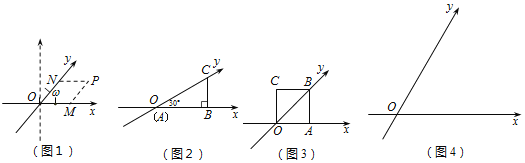
Œ“√«÷™µ¿£¨∆Ω√ʃ⁄ª•œý¥π÷±«“”–π´π≤‘≠µ„µƒ¡ΩÃı ˝÷·ππ≥…∆Ω√Ê÷±Ω«◊¯±Íœµ£Æ»Áπ˚¡ΩÃı ˝÷·≤ª¥π÷±£¨∂¯ «œýΩª≥…»Œ“‚µƒΩ«¶ÿ£®0°„£º¶ÿ£º180°„«“¶ÿ°Ÿ90°„£©£¨ƒ«√¥’‚¡ΩÃı ˝÷·ππ≥…µƒ «∆Ω√Ê–±◊¯±Íœµ£Æ»ÁÕº1£¨æ≠π˝∆Ω√ʃ⁄“ªµ„P◊˜◊¯±Í÷·µƒ∆Ω––œþPM∫ÕPNΩªx÷·∫Õy÷·”⁄M°¢N£¨µ„M°¢N‘⁄x÷·∫Õy÷·…œÀ˘∂‘”¶µƒ ˝∑÷±Ω–◊ˆPµ„µƒx◊¯±Í∫Õy◊¯±Í£Æ
»ÁÕº2£¨¶ÿ=30°„£¨÷±Ω«»˝Ω«–Œµƒ∂•µ„A‘⁄◊¯±Í‘≠µ„O£¨µ„B°¢C∑÷±‘⁄x÷·∫Õy÷·…œ£¨AB=![]() £¨‘Úµ„B°¢C‘⁄¥À–±◊¯±Íœµƒ⁄µƒ◊¯±Í∑÷±Œ™B £¨C £Æ
£¨‘Úµ„B°¢C‘⁄¥À–±◊¯±Íœµƒ⁄µƒ◊¯±Í∑÷±Œ™B £¨C £Æ
£®2£©≥¢ ‘”¶”√
»ÁÕº3£¨¶ÿ=45°„£¨OŒ™◊¯±Í‘≠µ„£¨±þ≥§Œ™1µƒ’˝∑Ω–ŒOABC“ª±þOA‘⁄x÷·…œ£¨…˵„G£®x£¨y£©‘⁄æ≠π˝A°¢C¡Ωµ„µƒ÷±œþ…œ£¨«Ûy”Îx÷ƺ‰¬˙◊„µƒπÿœµ Ω£Æ
£®3£©…Ó»ÎÃΩæø
»ÁÕº4£¨¶ÿ=60°„£¨OŒ™◊¯±Í‘≠µ„£¨M£®2£¨2£©£¨‘≤Mµƒ∞Îæ∂Œ™![]() £Æ”–“ª∏ˆƒ⁄Ω«Œ™60°„µƒ¡‚–Œ£¨¡‚–Œµƒ“ª±þ‘⁄x÷·…œ£¨¡Ì”–¡Ω±þÀ˘‘⁄÷±œþ«°∫√”Α≤Mœý«–£¨«Û¥À¡‚–Œµƒ±þ≥§£Æ
£Æ”–“ª∏ˆƒ⁄Ω«Œ™60°„µƒ¡‚–Œ£¨¡‚–Œµƒ“ª±þ‘⁄x÷·…œ£¨¡Ì”–¡Ω±þÀ˘‘⁄÷±œþ«°∫√”Α≤Mœý«–£¨«Û¥À¡‚–Œµƒ±þ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥–£Œ™¡À¡ÀΩ‚—ß…˙µƒ∞≤»´“‚ ∂£¨‘⁄»´–£∑∂Œßƒ⁄Àʪ˙≥È»°≤ø∑÷—ß…˙Ω¯––Œ æ̵˜≤È£Æ∏˘æðµ˜≤ÈΩ·π˚£¨∞——ß…˙µƒ∞≤»´“‚ ∂∑÷≥…°∞µ≠±°°±°¢°∞“ª∞„°±°¢°∞Ωœ«ø°±°¢°∞∫Ыø°±Àƒ∏ˆ≤„¥Œ£¨≤¢ªÊ÷∆≥…»Áœ¬¡Ω∑˘…–≤ªÕÍ’˚µƒÕ≥º∆Õº£Æ
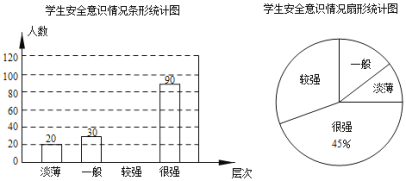
∏˘æð“‘…œ–≈œ¢£¨Ω‚¥œ¬¡–Œ £∫
£®1£©’‚¥Œµ˜≤È“ªπ≤≥È»°¡À°° °°√˚—ß…˙£¨Ω´Ãı–ŒÕ≥º∆Õº≤π≥‰ÕÍ’˚£ª
£®2£©…»–ŒÕ≥º∆Õº÷–£¨°∞Ωœ«ø°±≤„¥ŒÀ˘’º‘≤–ƒΩ«µƒ¥Û–°Œ™°° °°°„£ª
£®3£©»Ù∏√–£”–1800√˚—ß…˙£¨œ÷“™∂‘∞≤»´“‚ ∂Œ™°∞µ≠±°°±°¢°∞“ª∞„°±µƒ—ß…˙«øªØ∞≤»´ΩÔ˝£¨∏˘æðµ˜≤ÈΩ·π˚£¨«Îƒ„π¿º∆»´–£–Ë“™«øªØ∞≤»´ΩÔ˝µƒ—ß…˙»À ˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂˛¥Œ∫Ø ˝y£Ωax2+bx+c£®a°Ÿ0£©µƒÕºœÛµƒ∂‘≥∆÷· «÷±œþx£Ω1£¨∆‰ÕºœÛµƒ“ª≤ø∑÷»ÁÕºÀ˘ æ£Æœ¬¡–Àµ∑®¥ÌŒÛµƒ «
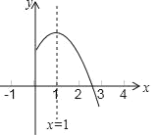
A. abc£º0B. a©Åb+c£º0C. 3a+c£º0D. µ±©Å1£ºx£º3 ±£¨y£æ0
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨µ„A£¨B£¨C£¨D∂º‘⁄°—O…œ£¨AC£¨BDœýΩª”⁄µ„E£¨‘Ú°œABD=£® £©
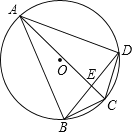
A. °œACD B. °œADB C. °œAED D. °œACB
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº¢Ÿ£¨‘⁄’˝∑Ω–ŒABCD÷–£¨µ„P—ÿ±þDA¥”µ„Dø™ ºœÚµ„A“‘1cm/sµƒÀŸ∂»“∆∂Ø£∫Õ¨ ±µ„Q—ÿ±þAB£¨BC¥”µ„Aø™ ºœÚµ„C“‘acm/sµƒÀŸ∂»“∆∂Ø£¨µ±µ„P“∆∂ØµΩµ„A ±£¨P£¨QÕ¨ ±Õ£÷π“∆∂أƅ˵„P≥ˆ∑¢x√Î ±£¨°˜PAQµƒ√ʪ˝Œ™ycm2£¨y”Îxµƒ∫Ø ˝ÕºœÛ»ÁÕº¢⁄£¨œþ∂ŒEFÀ˘‘⁄µƒ÷±œþ∂‘”¶µƒ∫Ø ˝πÿœµ ΩŒ™y£Ω©Å4x+21£¨‘Úaµƒ÷µŒ™£®°°°°£©
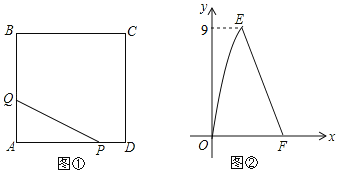
A. 1.5B. 2C. 3D. 4
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øºŸ∆⁄¿Ô£¨–°ª™∫Õ–°¡¡µΩƒ≥”∞≥«ø¥µÁ”∞£¨”∞≥«Õ¨ ±‘⁄Àƒ∏ˆ∑≈”≥ “£®1°¢2°¢3°¢4 “£©≤•∑≈Àƒ≤ø≤ªÕ¨µƒµÁ”∞£¨À˚√«∏˜◊‘‘⁄’‚Àƒ∏ˆ∑≈”≥ “»Œ—°“ª∏ˆ£¨√ø∏ˆ∑≈”≥ “±ª—°÷–µƒø…ƒÐ–‘∂ºœýÕ¨£Æ
£®1£©–°√˜—°‘Ò°∞1 “°±µƒ∏≈¬ Œ™°° °°£®÷±Ω”ÃÓø’£©
£®2£©”√ ˜◊¥ÕºªÚ¡–±Ìµƒ∑Ω∑®«Û–°ª™∫Õ–°¡¡—°‘Ò»•Õ¨“ªº‰∑≈”≥ “ø¥µÁ”∞µƒ∏≈¬ £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com