
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | x(x+1)=x2+x | B. | x2+2x+1=(x+1)2 | C. | x2+xy-3=x(x+y)-3 | D. | x2+6x+4=(x+3)2-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
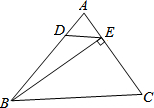 如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )
如图,锐角△ABC中,BE⊥AC,∠ADE=∠C,记△ADE的面积S1,△ABC的面积S2,则$\frac{S_1}{S_2}$=( )| A. | sin2A | B. | cos2A | C. | tan2A | D. | $\frac{1}{{{{tan}^2}A}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.1×105米 | B. | 2.1×106米 | C. | 0.21×106米 | D. | 21×104米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
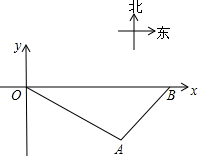 一艘轮船从O处出发,以30海里/时的速度沿东偏南30°的航线航行,两小时后到达A处.此时接到大风警报,轮船必须在1.5小时内赶到B处避风.B在O的正东方,从A处测得B的方位是北偏东45°.图所示的坐标系的单位长是1海里.
一艘轮船从O处出发,以30海里/时的速度沿东偏南30°的航线航行,两小时后到达A处.此时接到大风警报,轮船必须在1.5小时内赶到B处避风.B在O的正东方,从A处测得B的方位是北偏东45°.图所示的坐标系的单位长是1海里.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com