
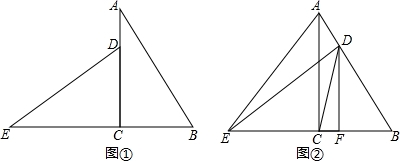
分析 (1)延长ED交AB于F,如图①,根据旋转的性质得∠A=∠E,再利用∠A+∠B=90°得到∠E+∠B=90°,则根据三角形内角和定理易得∠EFB=90°,于是利用垂直的定义可判断ED⊥AB;
(2)如图②,先利用平移的性质和(1)中的结论得到DE⊥AB,即∠ADE=90°,则利用圆周角定理的推论得到点C和点D在以AE为直径的圆上,然后根据圆周角定理即可得到结论.
解答 (1)解:ED⊥AB.理由如下: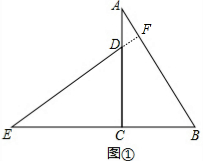
延长ED交AB于F,如图①,
∵Rt△ABC绕点C逆时针旋转90°,得到Rt△DEC,
∴∠A=∠E,
∵∠A+∠B=90°
∴∠E+∠B=90°
∴∠EFB=90°
∴ED⊥AB;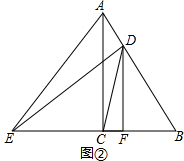
(2)证明:如图②,
∵将Rt△DEC沿CB方向向右平移,且使点D恰好落在AB边上,
∴DE⊥AB,
∴∠ADE=90°,
∵∠ACE=90°,
∴点C和点D在以AE为直径的圆上,
∴∠ACD=∠AED.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.解决(2)的关键是确定点C和点D在以AE为直径的圆上,从而利用圆周角定理求解.


科目:初中数学 来源: 题型:解答题
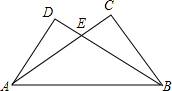 如图,在△ABC和△BAD中,AC与BD相交于点E,已知AD=BC,另外只能从下面给出的三个条件①∠DAB=∠CBA,②∠D=∠C ③∠DBA=∠CAB 选择其中的一个用来证明在△ABC和△BAD全等,这个条件是①.(填写编号),并证明△ABC≌△BAD.
如图,在△ABC和△BAD中,AC与BD相交于点E,已知AD=BC,另外只能从下面给出的三个条件①∠DAB=∠CBA,②∠D=∠C ③∠DBA=∠CAB 选择其中的一个用来证明在△ABC和△BAD全等,这个条件是①.(填写编号),并证明△ABC≌△BAD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
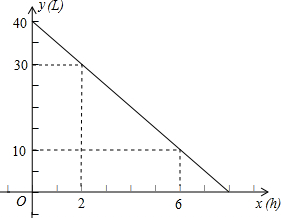 某种以汽油为燃料的机器,加满油并开始工作后,油箱中的余油量y(升)与工作时间x(小时)之间的函数关系如图所示.
某种以汽油为燃料的机器,加满油并开始工作后,油箱中的余油量y(升)与工作时间x(小时)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
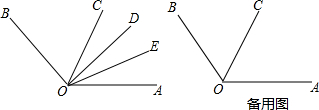 已知:OC平分∠AOB,以O为端点作射线OD,OE平分∠AOD,
已知:OC平分∠AOB,以O为端点作射线OD,OE平分∠AOD,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
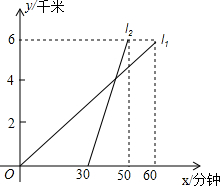 甲乙两车从A地出发,沿同一条公路行驶至距A地6千米的B地,l1、l2分别表示甲乙两车行驶路程y(千米)与时间x(分钟)之间的关系(如图所示).
甲乙两车从A地出发,沿同一条公路行驶至距A地6千米的B地,l1、l2分别表示甲乙两车行驶路程y(千米)与时间x(分钟)之间的关系(如图所示).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com