
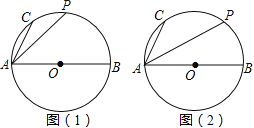
【题目】如图,AB是⊙O的直径,C、P是![]() 上两点,AB=13,AC=5,
上两点,AB=13,AC=5,
(1)如图(1),若点P是![]() 的中点,求PA的长;
的中点,求PA的长;
(2)如图(2),若点P是![]() 的中点,求PA得长 .
的中点,求PA得长 .
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)根据圆周角的定理,∠APB=90°,p是弧AB的中点,所以三角形APB是等腰三角形,利用勾股定理即可求得.
(2)根据垂径定理得出OP垂直平分BC,得出OP∥AC,从而得出△ACB∽△0NP,根据对应边成比例求得ON、AN的长,利用勾股定理求得NP的长,进而求得PA.
试题解析::(1)如答图(1),连接PB,
∵AB是⊙O的直径且P是![]() 的中点,∴∠PAB=∠PBA=45°,∠APB=90°.
的中点,∴∠PAB=∠PBA=45°,∠APB=90°.
又∵在等腰三角形△ABC中有AB=13,
∴![]() .
.
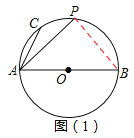
(2)如答图(2),连接BC,与OP相交于M点,作PH⊥AB于点H,
∵P点为![]() C的中点,∴OP⊥BC,∠OMB=90°,
C的中点,∴OP⊥BC,∠OMB=90°,
又∵AB为直径,∴∠ACB=90°.∴∠ACB=∠OMB. ∴OP∥AC.∴∠CAB=∠POB.
又∵∠ACB=∠OHP=90°,∴△ACB∽△0HP.∴![]() .
.
又∵![]() ,∴
,∴![]() ,解得
,解得![]() .
.
∴AH=OA+OH=9.
∵在Rt△OPH中,有![]() 。
。
∴在RT△AHP中 有![]() .
.
∴PA=![]() .
.


科目:初中数学 来源: 题型:
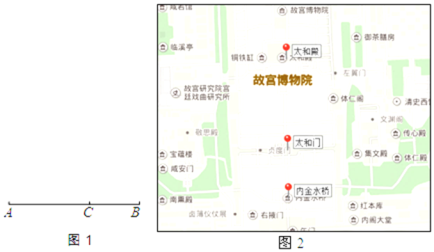
【题目】如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果BCAB=AC2,那么称线段AB被点C黄金分割.为了增加美感,黄金分割经常被应用在绘画、雕塑、音乐、建筑等艺术领域.如图2,在“附中博识课程中”,小白菜们沿着紫禁城的中轴线,从内金水桥走到了太和殿,领略了古代建筑的宏伟.太和门位于太和殿与内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割.已知太和殿到内金水桥的距离约为100丈,设太和门到太和殿之间的距离为x丈,要求x,则可列方程为________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象与y=x-1的图象平行,且经过点(2,6).
(1)求一次函数y=kx+b的表达式.
(2)求这个一次函数y=kx+b与坐标轴的两个交点坐标,并在直角坐标系中画出这个函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,O为坐标原点,点A(3,4),点B(6,0).
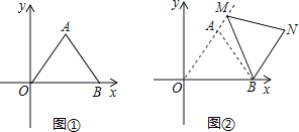
(1)如图①,求AB的长;
(2)如图2,把图①中的△ABO绕点B顺时针旋转,使O的对应点M恰好落在OA的延长线上,N是点A旋转后的对应点;
①求证:四边形AOBN是平行四边形;
②求点N的坐标.
(3)点C是OB的中点,点D为线段OA上的动点,在△ABO绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:对于一个关于![]() 的一元二次方程
的一元二次方程![]() (其中a≠0,a、b、c为常数)的两根分别为
(其中a≠0,a、b、c为常数)的两根分别为![]() ,
,![]() ,我们有如下发现①若
,我们有如下发现①若![]() ,
,![]() 为整数,则这个一元二次方程的判别式
为整数,则这个一元二次方程的判别式![]() 一定为完全平方数;②
一定为完全平方数;② ![]() ,
,![]() 满足韦达定理:即
满足韦达定理:即![]() ,
,![]() ;
;
③韦达定理也有逆定理,即如果两数![]() 和
和![]() 满足如下关系:
满足如下关系:![]() ,
,![]() ,那么这两个数
,那么这两个数![]() 和
和![]() 是方程
是方程![]() (
(![]() )的两个根.
)的两个根.
请应用上述材料解决以下问题:
(1)若实数![]() ,
,![]() 是关于
是关于![]() 的一元二次方程
的一元二次方程![]() 的两个根,
的两个根,
①当![]() 时,则
时,则![]() ,
,![]() ;
;
②若![]() 均为整数且
均为整数且![]() ,求
,求![]() 的值;
的值;
(2)已知实数![]() 满足
满足![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一块长方形镜面玻璃的四周,镶上与它的周长相等的边框,制成一面镜子.镜子的长与宽的比是3:1.已知镜面玻璃的价格是每平方米100元,边框的价格是每米20元,另外制作这面镜子还需加工费55元.如果制作这面镜子共花了210元,求这面镜子的长是__________![]() ,宽是___________
,宽是___________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某居民小区响应党的号召,开展全民健身活动.该小区准备修建一座健身馆,其设计方案如图所示,A区为成年人活动场所,B区为未成年人活动场所,其余地方均种花草.(π取3.14)
(1)活动场所和花草的面积各是多少?
(2)整座健身馆的面积是成年人活动场所面积的多少倍?
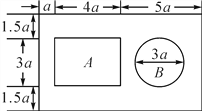
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com