

分析 (1)在BC上截取BG=CM,连接EG,如图1,根据等腰直角三角形的性质得∠A=∠B=45°,∠DEF=45°,再由E为AB的中点得CE=AE=BE,则∠ACE=45°,BC=$\sqrt{2}$CE,于是可利用“SAS”证明△MCE≌△GBE,得到EM=EG,∠1=∠2,接着证明∠4=45°,则根据“SAS”可判断△ENM≌△ENG,得到MN=GN,所以•BC=CN+NG+BG=CN+MN+CM,则有CN+MN+CM=$\sqrt{2}$CE;
(2)在AC上截取AH=CN,连接EH,如图2,易证得△AHE≌△CNE,得到EH=EN,∠AEH=∠CEN,由于∠CEN=∠CEM+∠MEN=∠CEM+45°,∠AEH+∠HCE=90°,得到∠HEC+∠CNM=90°-(∠CEM+45°)+∠CEM=45°,即有∠HEM=∠NEM,于是可根据“SAS”证明△EMH≌△EMN,得到MH=MN,则CH=MH-CM=MN-CM,所以AC=AH+CH=CN+MN-CM,由此得到CN+MN-CM=CE.
解答 解:(1)CN+MN+CM=$\sqrt{2}$CE.理由如下: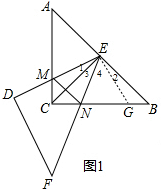
在BC上截取BG=CM,连接EG,如图1,
∵CA=CB,DE=DF,∠ACB=∠EDF=90°,
∴△ACB和△DEF都是等腰直角三角形,
∴∠A=∠B=45°,∠DEF=45°,
∵E为AB的中点,
∴CE=AE=BE,
∴∠ACE=45°,BC=$\sqrt{2}$CE,
在△MCE和△GBE中,
$\left\{\begin{array}{l}{CM=BG}&{\;}\\{∠MCE=∠B}&{\;}\\{CE=BE}&{\;}\end{array}\right.$,
∴△MCE≌△GBE(SAS),
∴EM=EG,∠1=∠2,
∵∠1+∠3=45°,
∴∠3+∠2=45°,
∴∠4=45°,
在△ENM和△ENG中,
$\left\{\begin{array}{l}{EN=EN}&{\;}\\{∠NEM=∠NEG}&{\;}\\{EM=EG}&{\;}\end{array}\right.$,
∴△ENM≌△ENG(SAS),
∴MN=GN,
∴BC=CN+NG+BG=CN+MN+CM,
∴CN+MN+CM=$\sqrt{2}$CE;
(2)CN+MN-CM=$\sqrt{2}$CE.理由如下: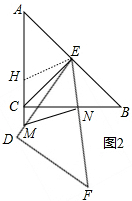
在AC上截取AH=CN,连接EH,如图2,
在△AHE和△CNE中,
$\left\{\begin{array}{l}{AH=CN}&{\;}\\{∠A=∠ECN}&{\;}\\{AE=CE}&{\;}\end{array}\right.$,
∴△AHE≌△CNE(SAS),
∴EH=EN,∠AEH=∠CEN,
而∠CEN=∠CEM+∠MEN=∠CEM+45°,
∠AEH+∠HCE=90°,
∴∠HEC+∠CEM=90°-(∠CEM+45°)+∠CEM=45°,
∴∠HEM=∠NEM,
在△EMH和△EMN中,
$\left\{\begin{array}{l}{EH=EN}&{\;}\\{∠HEN=∠NEM}&{\;}\\{EM=EM}&{\;}\end{array}\right.$,
∴△EMH≌△EMN(SAS),
∴MH=MN,
∴CH=MH-CM=MN-CM,
∴AC=AH+CH=CN+MN-CM,
∴CN+MN-CM=$\sqrt{2}$CE.
点评 本题考查了旋转的性质、等腰直角三角形的性质、全等三角形的判定与性质;熟练掌握旋转的性质和等腰直角三角形的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
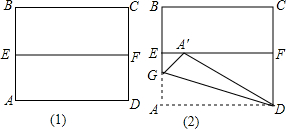 如图1,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线DG折叠,使A点落在EF上,对应点为A′,求∠DA′F的度数.
如图1,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线DG折叠,使A点落在EF上,对应点为A′,求∠DA′F的度数.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
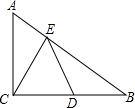 如图,在△ABC中,AC=BC=$\sqrt{5}$,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是$\frac{5}{2}$.
如图,在△ABC中,AC=BC=$\sqrt{5}$,∠ACB=90°,D是BC边的中点,E是AB边上一动点,则EC+ED的最小值是$\frac{5}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com