
【题目】如图,已知二次函数的图象与x轴交于A、B两点,D为顶点,其中点B的坐标为![]() ,点D的坐标为
,点D的坐标为![]() .
.

(1)求该二次函数的表达式;
(2)点E是线段BD上的一点,过点E作x轴的垂线,垂足为F,且![]() ,求点E的坐标.
,求点E的坐标.
(3)试问在该二次函数图象上是否存在点G,使得![]() 的面积是
的面积是![]() 的面积的
的面积的![]() ?若存在,求出点G的坐标;若不存在,请说明理由.
?若存在,求出点G的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)点E的坐标为
;(2)点E的坐标为![]() ;(3)存在,点G的坐标为
;(3)存在,点G的坐标为![]() 或
或![]() .
.
【解析】
(1)依题意,利用二次函数的顶点式即可求
(2)可通过点B,点D求出线段BD所在的直线关系式,点E在线段BD上,即可设点E的坐标,利用点与点的关系公式,通过![]() 即可求
即可求
(3)先求线段AD所在的直线解析式,求利用点到直线的公式![]() ,即可求
,即可求![]() 与
与![]() 的高,利用三角形面积公式即可求.
的高,利用三角形面积公式即可求.
(1)依题意,设二次函数的解析式为![]()
将点B代入得![]() ,得
,得![]()
∴二次函数的表达式为:![]()
(2)依题意,点![]() ,点
,点![]() ,设直线BD的解析式为
,设直线BD的解析式为![]()
代入得![]() ,解得
,解得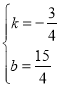
∴线段BD所在的直线为![]() ,
,
设点E的坐标为:![]()
∴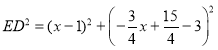
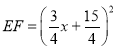
∵![]()
∴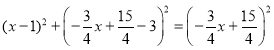
整理得![]()
解得![]() ,
,![]() (舍去)
(舍去)
故点E的纵坐标为![]()
∴点E的坐标为![]()
(3)存在点G,
设点G的坐标为![]()
∵点B的坐标为![]() ,对称轴
,对称轴![]()
∴点A的坐标为![]()
∴设AD所在的直线解析式为![]()
代入得![]() ,解得
,解得![]()
∴直线AD的解析式为![]()
∴ AD的距离为5
点G到AD的距离为:![]()
由(2)知直线BD的解析式为:![]() ,
,
∵BD的距离为5
∴同理得点G至BD的距离为:![]()
∴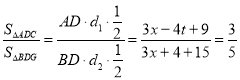
![]()
整理得![]()
∵点G在二次函数上,
∴![]()
代入得![]()
整理得![]()
解得![]() ,
,![]()
此时点G的坐标为![]() 或
或![]()


科目:初中数学 来源: 题型:
【题目】2018年高一新生开始,某省全面启动高考综合改革,实行“3+1+2”的高考选考方案.“3”是指语文、数学、外语三科必考;“1”是指从物理、历史两科中任选一科参加选考,“2”是指从政治、化学、地理、生物四科中任选两科参加选考
(1)“1+2”的选考方案共有多少种?请直接写出所有可能的选法;(选法与顺序无关,例如:“物、政、化”与“物、化、政”属于同一种选法)
(2)高一学生小明和小杰将参加新高考,他们酷爱历史和生物,两人约定必选历史和生物.他们还需要从政治、化学、地理三科中选一科参考,若这三科被选中的机会均等,请用列表或画树状图的方法,求出他们恰好都选中政治的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
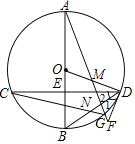
【题目】如图,在![]() 中,直径
中,直径![]() 经过弦
经过弦![]() 的中点
的中点![]() ,点
,点![]() 在
在![]() 上,
上,![]() 的延长线交于
的延长线交于![]() 于点
于点![]() ,交过
,交过![]() 的直线于
的直线于![]() ,
,![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若点![]() 是
是![]() 的中点,
的中点,![]() 的半径为3,
的半径为3,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
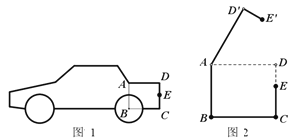
【题目】如图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD'E'的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.
(1)求点D'到BC的距离;
(2)求E、E'两点的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生到恩格贝![]() 和康镇
和康镇![]() 进行研学活动,澄澄老师在网上查得,
进行研学活动,澄澄老师在网上查得,![]() 和
和![]() 分别位于学校
分别位于学校![]() 的正北和正东方向,
的正北和正东方向,![]() 位于
位于![]() 南偏东37°方向,校车从
南偏东37°方向,校车从![]() 出发,沿正北方向前往
出发,沿正北方向前往![]() 地,行驶到15千米的
地,行驶到15千米的![]() 处时,导航显示,在
处时,导航显示,在![]() 处北偏东45°方向有一服务区
处北偏东45°方向有一服务区![]() ,且
,且![]() 位于
位于![]() ,
,![]() 两地中点处.
两地中点处.
(1)求![]() ,
,![]() 两地之间的距离;
两地之间的距离;
(2)校车从![]() 地匀速行驶1小时40分钟到达
地匀速行驶1小时40分钟到达![]() 地,若这段路程限速100千米/时,计算校车是否超速?
地,若这段路程限速100千米/时,计算校车是否超速?
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在-3、-2、-1、0、1、2,3,这七个数中,随机选取一个数,记为a,那么使得关于x的反比例函数![]() 的图像位于第一、三象限,且使得关于x的方程
的图像位于第一、三象限,且使得关于x的方程![]() 有整数解的概率为_____.
有整数解的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
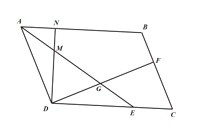
【题目】如图,已知□ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.
(1)求证:AM=GE
(2)若DG=a、CF=b,求AB的长.
(3)若![]() ,且DG=
,且DG=![]() ,直接写出CE的长.
,直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
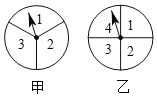
【题目】如图,甲、乙两个转盘分别被分成了![]() 等份与
等份与![]() 等份,每份内均标有数字.分别旋转这两个转盘,将转盘停止后指针所指区域内的两数相乘.
等份,每份内均标有数字.分别旋转这两个转盘,将转盘停止后指针所指区域内的两数相乘.
(1)请将所有可能出现的结果填入下表:
乙 积 甲 | 1 | 2 | 3 | 4 |
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
(2)积为![]() 的概率为 ;积为偶数的概率为 ;
的概率为 ;积为偶数的概率为 ;
(3)从![]() 这
这![]() 个整数中,随机选取
个整数中,随机选取![]() 个整数,该数不是(1)中所填数字的概率为 .
个整数,该数不是(1)中所填数字的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
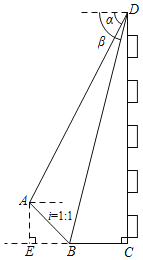
【题目】如图,某建筑物CD高96米,它的前面有一座小山,其斜坡AB的坡度为![]() .为了测量山顶A的高度,在建筑物顶端D处测得山顶A和坡底B的俯角分别为α、β.已知
.为了测量山顶A的高度,在建筑物顶端D处测得山顶A和坡底B的俯角分别为α、β.已知![]() ,
,![]() ,求山顶A的高度AE(C、B、E在同一水平面上).
,求山顶A的高度AE(C、B、E在同一水平面上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com