
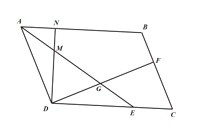
【题目】如图,已知□ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.
(1)求证:AM=GE
(2)若DG=a、CF=b,求AB的长.
(3)若![]() ,且DG=
,且DG=![]() ,直接写出CE的长.
,直接写出CE的长.
【答案】(1)见解析;(2)AB =a+b;(3)![]()
【解析】
(1)AE是∠BAD的角平分线 ,则∠BAE=∠DAE,四边形ABCD是平行四边形,则AB∥CD ,∠BAD=∠C,求得∠ADN=∠CDF,由AB∥CD知∠BAE=∠DEA,所以∠DAE=∠DEA,所以AD=DE.根据ASA证明△ADM≌△EDG,所以AM=EG.
(2) 过点A作HA⊥AD交DN的延长线于H,证明△DHA≌△DCF(ASA) , CF=AH=b DH=DC=AB.通过∠AMH=∠HAM,知HM=AH=CF=b .通过前面的全等知DM=DG =a,求得HD的长度.故知AB的长度.
(3) AB∥DC知对应线段成比例,由此可知![]() =
=![]() =
=![]() ,易得DN=
,易得DN=![]() , DA=DE 即AD=3AN, 在Rt△AND中,根据勾股定理可知
, DA=DE 即AD=3AN, 在Rt△AND中,根据勾股定理可知![]() , 由△ADN∽△CDF可知对应边成比例,可求得DC的长度,继而求得CE的长度.
, 由△ADN∽△CDF可知对应边成比例,可求得DC的长度,继而求得CE的长度.
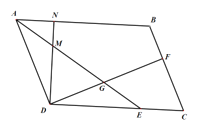
(1)证明:∵AE是∠BAD的平分线
∴ ∠BAE=∠DAE
∵DN⊥DC 、DF⊥BC
∴ ∠NDA=90° ∠DFC=90°
∵四边形ABCD是平行四边形
∴AB∥CD ∠BAD=∠C
∴∠DAE=∠DEA ∠ADN=∠EDG
∴ DA=DE
∴ △ADM≌△EDG(ASA)
∴AM=EG
(2)如图,过点A作HA⊥AD交DN的延长线于H.
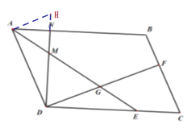
∴∠HAD=∠DFC=90°
∵∠ADH=∠FDC AD=DF
∴ △DHA≌△DCF(ASA)
∴CF=AH=b DH=DC=AB
易证 ∠AMH=∠HAM
∴HM=AH=CF=b
∵△ADM≌△EDG(已证)
∴DM=DG =a
∴AB=DC=DM+MH =a+b
(3) CE =DC-DE=![]() -2.
-2.
理由如下:
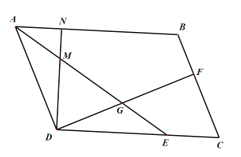
在□ABCD中,AB∥DC
∴![]() =
=![]() =
=![]() ,
,
∵ ![]() =
=![]() ∴
∴![]() =
=![]() =
=![]() ,
,
∵DG=DM=![]() ∴MN=
∴MN=![]() , 即
, 即![]()
∵ DA=DE 即AD=3AN,
∴在Rt△ADN中,![]()
![]()
易证:△ADN∽△CDF
∴![]()
即 ![]() =
=![]()
∴![]()
∴CE =DC-DE= ![]()


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
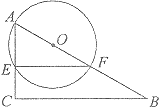
【题目】如图,![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 经过点
经过点![]() ,与
,与![]() 相交于点E,与
相交于点E,与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
(I).如图,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
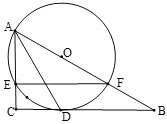
(II)如图,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() .
.
①求证:![]() 为
为![]() 的切线;
的切线;
②若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
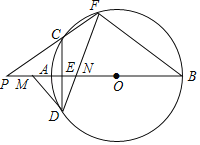
【题目】如图,![]() 是⊙
是⊙![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,点
,点![]() 是⊙
是⊙![]() 上一点,且
上一点,且![]() ,连接
,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
(1)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半径;
的半径;
(2)求证:![]() 为等腰三角形;
为等腰三角形;
(3)连接![]() 并延长,交
并延长,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数的图象与x轴交于A、B两点,D为顶点,其中点B的坐标为![]() ,点D的坐标为
,点D的坐标为![]() .
.

(1)求该二次函数的表达式;
(2)点E是线段BD上的一点,过点E作x轴的垂线,垂足为F,且![]() ,求点E的坐标.
,求点E的坐标.
(3)试问在该二次函数图象上是否存在点G,使得![]() 的面积是
的面积是![]() 的面积的
的面积的![]() ?若存在,求出点G的坐标;若不存在,请说明理由.
?若存在,求出点G的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
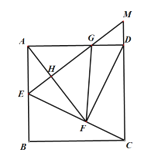
【题目】如图,在边长为10cm的正方形ABCD中,E为AB的中点,连接CE,过点D作![]() 于点
于点![]() ,连接AF,过点E作
,连接AF,过点E作![]() 于点H且交CD的延长线于点
于点H且交CD的延长线于点![]() ,交AD于点
,交AD于点![]() ,连接FG,则
,连接FG,则![]() =_____cm2.
=_____cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD的对角线AC上取一点E.使得![]() ,连接BE并延长BE到F,使
,连接BE并延长BE到F,使![]() ,BF与CD相交于点H,若
,BF与CD相交于点H,若![]() ,有下列结论:①
,有下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .则其中正确的结论有( )
.则其中正确的结论有( )
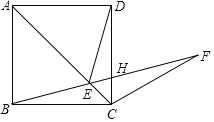
A. ①②③B. ①②③④C. ①②④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数
中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数![]() 的图象经过B、C两点.
的图象经过B、C两点.
(1)求该二次函数的解析式;
(2)将该二次函数图象向下平移几个单位,可使平移后所得图象经过坐标原点?直接写出平移后所得图象与x轴的另一个交点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索.画函数![]() 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数
的图象,经历分析解析式、列表、描点、连线过程得到函数图象如图所示;经历同样的过程画函数![]() 和
和![]() 的图象如图所示.
的图象如图所示.
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣6 | ﹣4 | ﹣2 | 0 | ﹣2 | ﹣4 | ﹣6 | … |
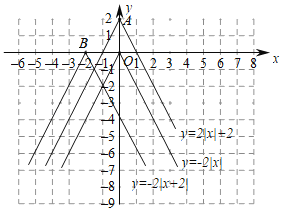
(1)观察发现:三个函数的图象都是由两条射线组成的轴对称图形;三个函数解折式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.写出点A,B的坐标和函数![]() 的对称轴.
的对称轴.
(2)探索思考:平移函数![]() 的图象可以得到函数
的图象可以得到函数![]() 和
和![]() 的图象,分别写出平移的方向和距离.
的图象,分别写出平移的方向和距离.
(3)拓展应用:在所给的平面直角坐标系内画出函数的图象.若点
![]() 和
和![]() 在该函数图象上,且
在该函数图象上,且![]() ,比较
,比较![]() ,
,![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xoy中(如图),已知一次函数的图像平行于直线![]() ,且经过点A(2,3),与x轴交于点B。
,且经过点A(2,3),与x轴交于点B。
(1)求这个一次函数的解析式;
(2)设点C在y轴上,当AC=BC时,求点C的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com