
【题目】如图,在平面直角坐标系![]() 中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数
中,边长为2的正方形OABC的顶点A、C分别在x轴、y轴的正半轴上,二次函数![]() 的图象经过B、C两点.
的图象经过B、C两点.
(1)求该二次函数的解析式;
(2)将该二次函数图象向下平移几个单位,可使平移后所得图象经过坐标原点?直接写出平移后所得图象与x轴的另一个交点的坐标.

科目:初中数学 来源: 题型:
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).
(1)请分别写出y1,y2与x之间的函数表达式.
(2)小亮一年内在此游泳馆游泳的次数x在什么范围时,选择方式一比方式二省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生到恩格贝![]() 和康镇
和康镇![]() 进行研学活动,澄澄老师在网上查得,
进行研学活动,澄澄老师在网上查得,![]() 和
和![]() 分别位于学校
分别位于学校![]() 的正北和正东方向,
的正北和正东方向,![]() 位于
位于![]() 南偏东37°方向,校车从
南偏东37°方向,校车从![]() 出发,沿正北方向前往
出发,沿正北方向前往![]() 地,行驶到15千米的
地,行驶到15千米的![]() 处时,导航显示,在
处时,导航显示,在![]() 处北偏东45°方向有一服务区
处北偏东45°方向有一服务区![]() ,且
,且![]() 位于
位于![]() ,
,![]() 两地中点处.
两地中点处.
(1)求![]() ,
,![]() 两地之间的距离;
两地之间的距离;
(2)校车从![]() 地匀速行驶1小时40分钟到达
地匀速行驶1小时40分钟到达![]() 地,若这段路程限速100千米/时,计算校车是否超速?
地,若这段路程限速100千米/时,计算校车是否超速?
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
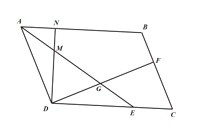
【题目】如图,已知□ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.
(1)求证:AM=GE
(2)若DG=a、CF=b,求AB的长.
(3)若![]() ,且DG=
,且DG=![]() ,直接写出CE的长.
,直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比乙种水果的进价每千克少4元,且用800元购进甲种水果的数量与用1000元购进乙种水果的数量相同.
(1)求甲、乙两种水果的单价分别是多少元?
(2)该水果商根据该水果店平常的销售情况确定,购进两种水果共200千克,其中甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,购回后,水果商决定甲种水果的销售价定为每千克20元,乙种水果的销售价定为每千克25元,则水果商应如何进货,才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
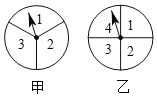
【题目】如图,甲、乙两个转盘分别被分成了![]() 等份与
等份与![]() 等份,每份内均标有数字.分别旋转这两个转盘,将转盘停止后指针所指区域内的两数相乘.
等份,每份内均标有数字.分别旋转这两个转盘,将转盘停止后指针所指区域内的两数相乘.
(1)请将所有可能出现的结果填入下表:
乙 积 甲 | 1 | 2 | 3 | 4 |
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
(2)积为![]() 的概率为 ;积为偶数的概率为 ;
的概率为 ;积为偶数的概率为 ;
(3)从![]() 这
这![]() 个整数中,随机选取
个整数中,随机选取![]() 个整数,该数不是(1)中所填数字的概率为 .
个整数,该数不是(1)中所填数字的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,![]() .在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角
.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角![]() 为
为![]() (点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)
(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)![]() ,那么建筑物AB的高度约为( )
,那么建筑物AB的高度约为( )
(参考数据![]() ,
,![]() ,
,![]() )
)
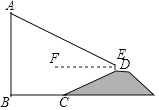
A.65.8米B.71.8米C.73.8米D.119.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成下面的统计图.
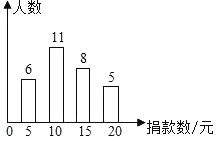
(1)本次调查的样本容量是________,这组数据的众数为________元;
(2)求这组数据的平均数;
(3)该校共有![]() 学生参与捐款,请你估计该校学生的捐款总数.
学生参与捐款,请你估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
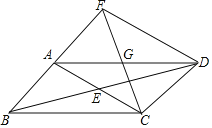
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com