
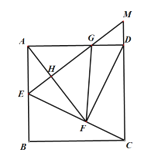
【题目】如图,在边长为10cm的正方形ABCD中,E为AB的中点,连接CE,过点D作![]() 于点
于点![]() ,连接AF,过点E作
,连接AF,过点E作![]() 于点H且交CD的延长线于点
于点H且交CD的延长线于点![]() ,交AD于点
,交AD于点![]() ,连接FG,则
,连接FG,则![]() =_____cm2.
=_____cm2.
【答案】![]()
【解析】
在Rt△BEC中,得出CE的长度,继而证明△EBC∽△CFD,根据相似三角形对应边成比例得出CF,CE的长度,故EF的长度.作PF⊥BE,易证△EPF∽△EBC,相似三角形对应边成比例,得AP=AE+EP=5+3=8 PF=6,AF=10,再证△AEH∽APF,得AH=4,EH=3. 最后证明△AEH∽AHG,![]() =EHHG,得出HG的长度,即可得到S△AGF.
=EHHG,得出HG的长度,即可得到S△AGF.

AB=BC=CD=10,
E是中点,BE=5,
在Rt△BEC中,CE=![]() =5
=5![]() ,
,
∠ECB=∠CDF,∠B=∠DFC,
∴△EBC∽△CFD.
∴![]() =
=![]() =
=![]() ,
,
∴CF=2![]() ,CE=5
,CE=5![]() ,EF=3
,EF=3![]() .
.
作PF⊥BE,∠B=90°
∵PF∥BC,
∴△EPF∽△EBC,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴PF=6,EP=3.
∴AP=AE+EP=5+3=8 PF=6,
∴AF=10,
∵EH![]() ,
,
∠EAH=∠FAP,∠APF=∠AHE,
∴△AEH∽△AFP,
∴![]() =
=![]() =
=![]() ,
,
![]() =
=![]() =
=![]() ,
,
AH=4,EH=3.
在△AEH和△AHG中,
∠EAH=∠AGH,∠AHE=∠GHA,
∴△AEH∽△GAH.
∴![]() =EHHG,
=EHHG,
∴HG=![]() ,
,
∴S△AGF=![]() AFHG
AFHG
=![]() ×
×![]()
=![]() .
.


科目:初中数学 来源: 题型:
【题目】甲、乙两家商场平时以同样价格出售相同的商品.春节期间两家商场都让利酬宾,其中甲商场所有商品按8折出售,乙商场对一次购物中不超过200元的不打折,超过200元后的价格部分打7折.
设商品原价为x元,顾客购物金额为y元.
(I).根据题意,填写下表:
商品原价 | 100 | 150 | 250 | … |
甲商场购物金额(元) | 80 | … | ||
乙商场购物金额(元) | 100 | … |
(Ⅱ).分别就两家商场的让利方式写出y关于x的函数关系式;
(Ⅲ).若x≥500时,选择哪家商场去购物更省钱?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数 | 30 | 75 | 130 | 210 | 480 | 856 | 1250 | 2300 |
发芽数 | 28 | 72 | 125 | 200 | 457 | 814 | 1187 | 2185 |
发芽频率 | 0.9333 | 0.9600 | 0.9615 | 0.9524 | 0.9521 | 0.9509 | 0.9496 | 0.9500 |
依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是_____(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生到恩格贝![]() 和康镇
和康镇![]() 进行研学活动,澄澄老师在网上查得,
进行研学活动,澄澄老师在网上查得,![]() 和
和![]() 分别位于学校
分别位于学校![]() 的正北和正东方向,
的正北和正东方向,![]() 位于
位于![]() 南偏东37°方向,校车从
南偏东37°方向,校车从![]() 出发,沿正北方向前往
出发,沿正北方向前往![]() 地,行驶到15千米的
地,行驶到15千米的![]() 处时,导航显示,在
处时,导航显示,在![]() 处北偏东45°方向有一服务区
处北偏东45°方向有一服务区![]() ,且
,且![]() 位于
位于![]() ,
,![]() 两地中点处.
两地中点处.
(1)求![]() ,
,![]() 两地之间的距离;
两地之间的距离;
(2)校车从![]() 地匀速行驶1小时40分钟到达
地匀速行驶1小时40分钟到达![]() 地,若这段路程限速100千米/时,计算校车是否超速?
地,若这段路程限速100千米/时,计算校车是否超速?
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程mx2+3x+1=0有两个不相等的实数根,则m的取值范围为( )
A. m<![]() B. m<
B. m<![]() 且m≠0C. m≤
且m≠0C. m≤![]() D. m≤
D. m≤![]() 且m≠0
且m≠0
查看答案和解析>>
科目:初中数学 来源: 题型:
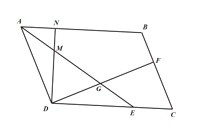
【题目】如图,已知□ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.
(1)求证:AM=GE
(2)若DG=a、CF=b,求AB的长.
(3)若![]() ,且DG=
,且DG=![]() ,直接写出CE的长.
,直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商计划购进甲、乙两种水果进行销售,经了解,甲种水果的进价比乙种水果的进价每千克少4元,且用800元购进甲种水果的数量与用1000元购进乙种水果的数量相同.
(1)求甲、乙两种水果的单价分别是多少元?
(2)该水果商根据该水果店平常的销售情况确定,购进两种水果共200千克,其中甲种水果的数量不超过乙种水果数量的3倍,且购买资金不超过3420元,购回后,水果商决定甲种水果的销售价定为每千克20元,乙种水果的销售价定为每千克25元,则水果商应如何进货,才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
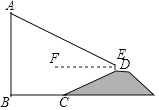
【题目】如图,AB是垂直于水平面的建筑物.为测量AB的高度,小红从建筑物底端B点出发,沿水平方向行走了52米到达点C,然后沿斜坡CD前进,到达坡顶D点处,![]() .在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角
.在点D处放置测角仪,测角仪支架DE高度为0.8米,在E点处测得建筑物顶端A点的仰角![]() 为
为![]() (点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)
(点A,B,C,D,E在同一平面内).斜坡CD的坡度(或坡比)![]() ,那么建筑物AB的高度约为( )
,那么建筑物AB的高度约为( )
(参考数据![]() ,
,![]() ,
,![]() )
)
A.65.8米B.71.8米C.73.8米D.119.8米
查看答案和解析>>
科目:初中数学 来源: 题型:
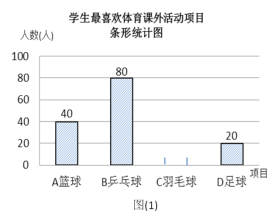
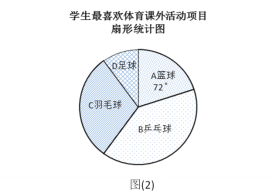
【题目】某学校为了丰富学生课余生活,决定开设以下体育课外活动项目:A篮球;B乒乓球;C羽毛球;D足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有__________人;
(2)请你将条形统计图(1)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com