
【题目】如图,![]() 是⊙
是⊙![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,点
,点![]() 是⊙
是⊙![]() 上一点,且
上一点,且![]() ,连接
,连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
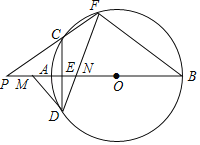
(1)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半径;
的半径;
(2)求证:![]() 为等腰三角形;
为等腰三角形;
(3)连接![]() 并延长,交
并延长,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() .求证:
.求证:![]() .
.
【答案】(1)⊙![]() 的半径为5;(2)详见解析;(3)详见解析.
的半径为5;(2)详见解析;(3)详见解析.
【解析】
(1)连接BC,AC,AD,通过证明△ACE∽△CEB,可得![]() ,可求BE的长,即可求⊙O的半径;
,可求BE的长,即可求⊙O的半径;
(2)通过证明△ADE≌△NDE,可得∠DAN=∠DNA,即可证BN=BF,可得△BNF为等腰三角形;
(3)通过证明△ODE∽△ODM,可得DO2=OEOM,通过证明△PCO∽△CEO,可得CO2=POON,即可得结论.
解:(1)如图1,连接![]() ,
,

∵![]() ,
,![]() 是直径
是直径
∴![]() ,
,![]()
∴![]() ,且
,且![]()
∴![]() ∽
∽![]()
∴![]()
∴![]()
∴![]()
∴![]()
∴⊙![]() 的半径为5
的半径为5
(2)∵![]()
∴![]() ,且
,且![]() ,
,![]()
∴![]() ≌
≌![]() (
(![]() )
)
∴![]() ,
,![]()
∵![]() ,
,![]()
∴![]()
∴![]() ,
,
∴![]() 是等腰三角形
是等腰三角形
(3)如图2,连接![]() ,
,

∵![]() 是切线,
是切线,
∴![]() ,
,
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]() ,
,
∴![]() ,
,
∵![]()
∴![]()
∵![]()
∴![]()
∵四边形![]() 是圆内接四边形
是圆内接四边形
∴![]()
∴![]() ,且
,且![]()
∴![]() ∽
∽![]()
∴![]()
∴![]() ,
,
∴![]() .
.


 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源: 题型:
【题目】解不等式组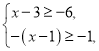
![]() 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_______________;
(Ⅱ)解不等式②,得_______________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来;
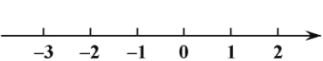
(Ⅳ)原不等式组的解集为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游泳馆推出了两种收费方式.
方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.
方式二:顾客不购买会员卡,每次游泳付费40元.设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).
(1)请分别写出y1,y2与x之间的函数表达式.
(2)小亮一年内在此游泳馆游泳的次数x在什么范围时,选择方式一比方式二省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
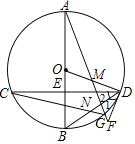
【题目】如图,在![]() 中,直径
中,直径![]() 经过弦
经过弦![]() 的中点
的中点![]() ,点
,点![]() 在
在![]() 上,
上,![]() 的延长线交于
的延长线交于![]() 于点
于点![]() ,交过
,交过![]() 的直线于
的直线于![]() ,
,![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若点![]() 是
是![]() 的中点,
的中点,![]() 的半径为3,
的半径为3,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果.下面是这个兴趣小组在相同的实验条件下,对某植物种子发芽率进行研究时所得到的数据:
种子数 | 30 | 75 | 130 | 210 | 480 | 856 | 1250 | 2300 |
发芽数 | 28 | 72 | 125 | 200 | 457 | 814 | 1187 | 2185 |
发芽频率 | 0.9333 | 0.9600 | 0.9615 | 0.9524 | 0.9521 | 0.9509 | 0.9496 | 0.9500 |
依据上面的数据可以估计,这种植物种子在该实验条件下发芽的概率约是_____(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
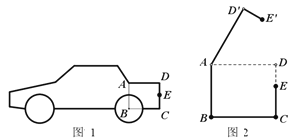
【题目】如图1是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角为60°时,箱盖ADE落在AD'E'的位置(如图2所示).已知AD=90厘米,DE=30厘米,EC=40厘米.
(1)求点D'到BC的距离;
(2)求E、E'两点的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生到恩格贝![]() 和康镇
和康镇![]() 进行研学活动,澄澄老师在网上查得,
进行研学活动,澄澄老师在网上查得,![]() 和
和![]() 分别位于学校
分别位于学校![]() 的正北和正东方向,
的正北和正东方向,![]() 位于
位于![]() 南偏东37°方向,校车从
南偏东37°方向,校车从![]() 出发,沿正北方向前往
出发,沿正北方向前往![]() 地,行驶到15千米的
地,行驶到15千米的![]() 处时,导航显示,在
处时,导航显示,在![]() 处北偏东45°方向有一服务区
处北偏东45°方向有一服务区![]() ,且
,且![]() 位于
位于![]() ,
,![]() 两地中点处.
两地中点处.
(1)求![]() ,
,![]() 两地之间的距离;
两地之间的距离;
(2)校车从![]() 地匀速行驶1小时40分钟到达
地匀速行驶1小时40分钟到达![]() 地,若这段路程限速100千米/时,计算校车是否超速?
地,若这段路程限速100千米/时,计算校车是否超速?
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
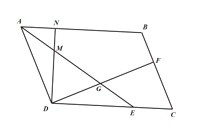
【题目】如图,已知□ABCD中,AE平分∠BAD交DC于E,DF⊥BC于F,交AE于G,且AD=DF.过点D作DC的垂线,分别交AE、AB于点M、N.
(1)求证:AM=GE
(2)若DG=a、CF=b,求AB的长.
(3)若![]() ,且DG=
,且DG=![]() ,直接写出CE的长.
,直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成下面的统计图.
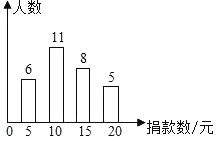
(1)本次调查的样本容量是________,这组数据的众数为________元;
(2)求这组数据的平均数;
(3)该校共有![]() 学生参与捐款,请你估计该校学生的捐款总数.
学生参与捐款,请你估计该校学生的捐款总数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com