
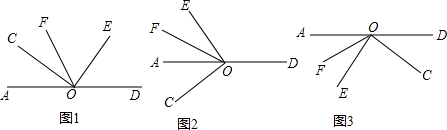
分析 (1)根据已知条件和图形可知:∠COE=90°,∠COE+∠AOC+∠DOE=180°,从而可以得到∠AOC与∠DOE的数量关系;由射线OF平分∠AOE,∠AOC与∠DOE的数量关系,从而可以得到∠COF和∠DOE的数量关系;
(2)由图2,可以得到各个角之间的关系,从而可以得到∠COF和∠DOE之间的数量关系;
(3)由图3和已知条件可以建立各个角之间的关系,从而可以得到∠COF和∠DOE之间的数量关系.
解答 解:(1)∵∠COE=90°,∠COE+∠AOC+∠DOE=180°,
∴∠AOC+∠DOE=90°,
∵射线OF平分∠AOE,
∴∠AOF=∠EOF=$\frac{1}{2}$∠AOE,
∴∠COF=∠AOF-∠AOC=$\frac{1}{2}$∠AOE-(90°-∠DOE)=$\frac{1}{2}(180°-∠DOE)-90°+∠DOE$=$\frac{1}{2}∠DOE$,
故答案为:互余,$∠COF=\frac{1}{2}∠DOE$;
(2)$∠COF=\frac{1}{2}∠DOE$
∵OF平分∠AOE,
∴$∠AOF=\frac{1}{2}∠AOE$,
∵∠COE=90°,
∴∠AOC=90°-∠AOE,
∴∠COF=∠AOC+∠AOF=90°-∠AOE+$\frac{1}{2}$∠AOE=90°-$\frac{1}{2}$∠AOE,
∵∠AOE=180°-∠DOE,
∴∠COF=90°-$\frac{1}{2}$(180°-∠DOE)=$\frac{1}{2}$∠DOE,
即$∠COF=\frac{1}{2}∠DOE$;
(3)$∠COF=180°-\frac{1}{2}∠DOE$.
∵OF平分∠AOE,
∴$∠EOF=\frac{1}{2}∠AOE$,
∴∠COF=∠COE+∠EOF=90°+$\frac{1}{2}∠AOE$=90°+$\frac{1}{2}(180°-∠DOE)$=180°-$\frac{1}{2}∠DOE$,
即$∠COF=180°-\frac{1}{2}∠DOE$.
点评 本题考查角的计算,解题的关键是找出各个角之间的关系,利用数形结合的思想找出所求问题需要的条件.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:选择题
| A. | a元 | B. | 0.7a元 | C. | 1.05a元 | D. | 0.93a元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
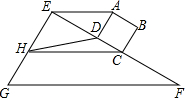 如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形ABCD的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5.
如图,正方形ABCD的边CD与Rt△EFG的直角边EF重合,将正方形ABCD以1cm/s的速度沿FE方向移动,在移动过程中,边CD始终与边EF重合(移动开始时点C与点F重合).连接AE,过点C作AE的平行线交直线EG于点H,连接HD.已知正方形ABCD的边长为1cm,EF=4cm,设正方形移动时间为x(s),线段EH的长为y(cm),其中0≤x≤2.5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
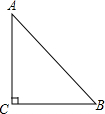 如果三角形有一个边上的中线长恰好等于这个边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣中线”.如图,在△ABC中,∠C=90°,较短的一条直角边BC=1,且△ABC是“有趣三角形”,求△ABC的“有趣中线”的长.
如果三角形有一个边上的中线长恰好等于这个边的长,那么称这个三角形是“有趣三角形”,这条中线为“有趣中线”.如图,在△ABC中,∠C=90°,较短的一条直角边BC=1,且△ABC是“有趣三角形”,求△ABC的“有趣中线”的长.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com