
分析 设l与t的函数关系式为l=kt+b,将(0,12)和(50,12.01)代入求得函数关系式后把t=100代入解答即可.
解答 解:设l与t的函数关系式为l=kt+b,
可得:$\left\{\begin{array}{l}{b=12}\\{12.01=50k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=0.0002}\\{b=12}\end{array}\right.$,
所以l与t的函数关系式为l=0.0002t+12;
把t=100代入l=0.0002t+12=12.02,
故答案为:12.02
点评 本题考查了一次函数与实际结合的问题,同学们应能够列函数解析式,并能够求出对应的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
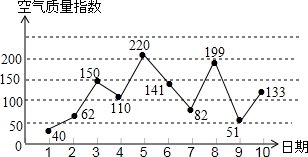 如图是某市11月1日至10日的空气质量指数折线图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择11月1日至11月7日中的某一天到达该市旅游,到达的当天作为第一天连续停留4天.则此人在该市停留期间恰好有两天空气质量优良的概率是( )
如图是某市11月1日至10日的空气质量指数折线图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择11月1日至11月7日中的某一天到达该市旅游,到达的当天作为第一天连续停留4天.则此人在该市停留期间恰好有两天空气质量优良的概率是( )| A. | $\frac{2}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{2}{5}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
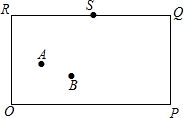 下面设想用电脑模拟台球游戏,为简单起见,约定:
下面设想用电脑模拟台球游戏,为简单起见,约定:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
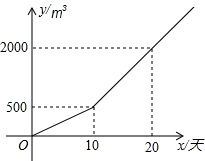 某农户种植一种经济作物,总量用水量y(m3)与种植时间x(天)之间的函数关系如图所示.
某农户种植一种经济作物,总量用水量y(m3)与种植时间x(天)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
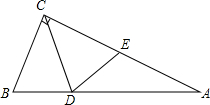 如图,在直角三角形ABC中,∠BCA=90°,BC=3,D为AB上一点,连接CD,如果三角形BCD沿直线CD翻折后,点B恰好与边AC的中点E重合,那么点D到直线AC的距离为2.
如图,在直角三角形ABC中,∠BCA=90°,BC=3,D为AB上一点,连接CD,如果三角形BCD沿直线CD翻折后,点B恰好与边AC的中点E重合,那么点D到直线AC的距离为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
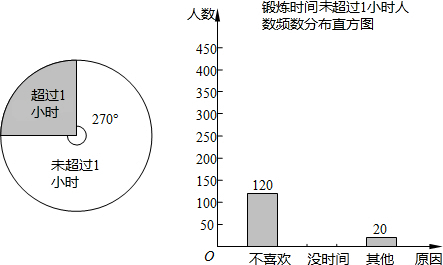
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com