

���� ��˼������֤����ͼ1�������D�ڡ�O�ڣ��ӳ�AD����O�ڵ�E������BE�����AEB=��ACB��������ǵ����ʵõ���ADB����AEB�����ǵõ���ADB����ACB�����ǵõ����ۣ�
��Ӧ�á���1���������֪��AC=AD����CAD=�������ݵ��������ε����ʼ��ɵõ���ACD=90��-$\frac{1}{2}��$��
��2�����ݵ��������ε����ʵõ���ABE=90��-$\frac{1}{2}$����ͬʱ���ġ�ACD=��ABE�����ɵõ����ۣ�
��3����B��C��A��F�ĵ㹲Բ���õ���BFA+��BCA=180�㣬�Ƴ�AF��BE�����ݵ��������ε����ʼ��ɵõ����ۣ�
��� 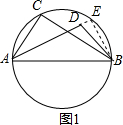 ��˼������֤����ͼ1�������D�ڡ�O�ڣ��ӳ�AD����O�ڵ�E������BE�����AEB=��ACB��
��˼������֤����ͼ1�������D�ڡ�O�ڣ��ӳ�AD����O�ڵ�E������BE�����AEB=��ACB��
�ߡ�ADB�ǡ�BDE����ǣ�
���ADB����AEB��
���ADB����ACB��
��ˣ���ADB����ACB����������ACB=��ADBì�ܣ�
���DҲ���ڡ�O�ڣ�
���D�����ڡ�O�ڣ�Ҳ���ڡ�O�⣬��D�ڡ�O�ϣ�
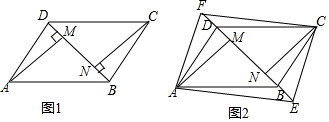
��Ӧ�á���1���������֪��AC=AD����CAD=����
���ACD=90��-$\frac{1}{2}��$��
��2����AB=AE����BAE=�������ABE=90��-$\frac{1}{2}$�������ACD=��ABE��
��B��C��A��F�ĵ㹲Բ��
��3����B��C��A��F�ĵ㹲Բ��
���BFA+��BCA=180�㣬
�֡ߡ�ACB=90�㣬
���BFA=90�㣬
��AF��BE��
��AB=AE��
��BF=EF��
����FΪBE���е㣮
���� ���⿼����ǵ���Բ��λ�ù�ϵ��Բ�ܽǶ����Լ���֤����Ӧ�ã����շ�֤����һ�㲽�衢ͬ�����Ե�Բ�ܽ�����ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����ʾ����綯�����Ҽ�ʻ����������ʻ120km�Ĺ�������ʻ��·��y�뾭����ʱ��x֮��ĺ���ͼ�������ͼ�����������⣺
��ͼ��ʾ����ʾ����綯�����Ҽ�ʻ����������ʻ120km�Ĺ�������ʻ��·��y�뾭����ʱ��x֮��ĺ���ͼ�������ͼ�����������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com