Question

【题目】如图，在Rt△ABC中，∠BAC＝90°，AD⊥BC于D，BE平分∠ABC交AC于E，交AD于F，FG∥BC，FH∥AC，下列结论：①AE＝AF；②AF＝FH；③AG＝CE；④AB＋FG＝BC，其中正确的结论有________________．(填序号)

Answer 1

【答案】①②③④

【解析】

①正确.

∵∠BAC＝90°

∴∠ABE+∠AEB=90°

∴∠ABE=90°-∠AEB

∵AD⊥BC

∴∠ADB=90°

∴∠DBE+∠BFD=90°

∴∠DBE=90-∠BFD

∵∠BFD=∠AFE

∴∠DBE=90°-∠AFE

∵BE平分∠ABC

∴∠ABE=∠DBE

∴90°-∠AEB=90°-∠AFE

∴∠AEB=∠AFE

∴AE=AF

②正确.

∵∠BAC=90°

∴∠BAF+∠DAC=90°

∴∠BAF=90°-∠DAC

∵AD⊥BC

∴∠ADC=90°

∴∠C+∠DAC=90°

∴∠C=90°-∠DAC

∴∠C=∠BAF

∵FH∥AC

∴∠C=∠BHF

∴∠BAF=∠BHF

在△ABF和△HBF中

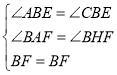
∴△ABF≌△HBF

∴AF=FH

③正确.

∵AE=AF，AF=FH

∴AE=FH

∵FG∥BC，FH∥AC

∴四边形FHCG是平行四边形

∴FH=GC

∴AE=GC

∴AE+EG=GC+EG

∴AG=CE

④正确.

∵四边形FHCG是平行四边形

∴FG=HC

∵△ABF≌△HBF

∴AB=HB

∴AB+FG=HB+HC=BC

故正确的答案有①②③④.