
【题目】如图,抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() (﹣1,0)、
(﹣1,0)、![]() (3,0),与
(3,0),与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 为线段
为线段![]() 上的动点(不与
上的动点(不与![]() 、
、![]() 重合),过点
重合),过点![]() 垂直于
垂直于![]() 轴的直线与抛物线及线段
轴的直线与抛物线及线段![]() 分别交于点
分别交于点![]() 、
、![]() ,点
,点![]() 在
在![]() 轴正半轴上,
轴正半轴上,![]() =2,连接
=2,连接![]() 、
、![]() .
.
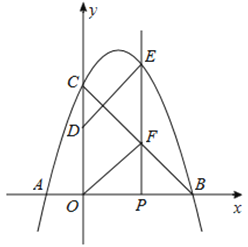
(1)求抛物线的解析式;
(2)当四边形![]() 是平行四边形时,求点
是平行四边形时,求点![]() 的坐标;
的坐标;
(3)过点![]() 的直线将(2)中的平行四边形
的直线将(2)中的平行四边形![]() 分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
分成面积相等的两部分,求这条直线的解析式.(不必说明平分平行四边形面积的理由)
【答案】(1)抛物线的解析式为:![]() ;(2)
;(2)![]() 点坐标为
点坐标为![]() 或
或![]() ;(3) ①当
;(3) ①当![]()
![]() 时,所求直线的解析式为:
时,所求直线的解析式为:![]() ;②当
;②当![]()
![]() 时,所求直线的解析式为:
时,所求直线的解析式为:![]() .
.
【解析】
(1)将点![]() 和点
和点![]() 的坐标代入抛物线函数中,可求出未知量
的坐标代入抛物线函数中,可求出未知量![]() ,
,![]() .则可求出该抛物线解析式;
.则可求出该抛物线解析式;
(2)由平行四边形的性质可知,![]() ,用含未知量
,用含未知量![]() 的代数式表示
的代数式表示![]() 的长度.则可得点
的长度.则可得点![]() 坐标 ;
坐标 ;
(3)平行四边形是中心对称图形,其对称中心为两条对角线的交点(或对角线的中点),过对称中心的直线平分平行四边形的面积,因此过点![]() 与
与![]() 对称中心的直线平分
对称中心的直线平分![]() 的面积.求得此直线,首先要求得
的面积.求得此直线,首先要求得![]() 对称中心的坐标.则两点坐标可确定该直线.
对称中心的坐标.则两点坐标可确定该直线.
解:(1)![]() 点
点![]()
![]() 、
、![]()
![]() 在抛物线
在抛物线![]() 上,
上,
∴![]() ,
,
解得![]() ,
,![]() ,
,
![]() 抛物线的解析式为:
抛物线的解析式为:![]() .
.
(2)在抛物线解析式![]() 中,令x=0,得y=3,
中,令x=0,得y=3,
∴C(0,3).
设直线BC的解析式为y=kx+b,,将![]()
![]() ,C
,C![]() 坐标代入得:
坐标代入得:
![]() ,
,
解得k=-1,b=3,
∴![]() .
.
设E点坐标为(x,-x2+2x+3),则P(x,0),F(x,-x+3),
∴EF=yE-yF=-x2+2x+3-(-x+3)=-x2+3x.
∵四边形ODEF是平行四边形,
∴EF=OD=2,
∴-x2+3x=2,即x2-3x+2=0,
解得x=1或x=2,
∴P点坐标为(1,0)或(2,0).
(3)平行四边形是中心对称图形,其对称中心为两条对角线的交点(或对角线的中点),过对称中心的直线平分平行四边形的面积,因此过点A与ODEF对称中心的直线平分ODEF的面积.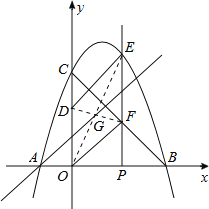
①当P(1,0)时,
点F坐标为(1,2),又D(0,2),
设对角线DF的中点为G,则![]() ,
,
设直线AG的解析式为y=kx+b,将A(-1,0),![]() 坐标代入得:
坐标代入得:
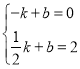
解得![]()
∴所求直线的解析式为:![]()
②当P
点F坐标为(2,1),又D(0,2),
设对角线DF的中点为G,则![]()
设直线AG的解析式为y=kx+b,将A(-1,0),![]() 坐标代入得:
坐标代入得:
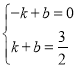
解得![]()
∴所求直线的解析式为:![]()
综上所述,所求直线的解析式为:![]() 或
或![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)
(1)请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1;
(2)请画出△ABC关于原点O成中心对称的图形△A2B2C2;
(3)在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标.
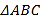
查看答案和解析>>
科目:初中数学 来源: 题型:
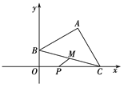
【题目】在平面直角坐标系中,点C、B分别在![]() 轴、
轴、![]() 轴上,△ABC是等腰直角三角形,∠BAC=90°,已知A(2,2)、P(1,0).M为BC的中点,则PM的最小值为_____.
轴上,△ABC是等腰直角三角形,∠BAC=90°,已知A(2,2)、P(1,0).M为BC的中点,则PM的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
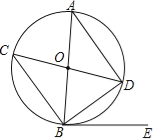
【题目】如图,在⊙O中,AB,CD是直径,BE是切线,B为切点,连接AD,BC,BD.
(1)求证:△ABD≌△CDB;
(2)若∠DBE=37°,求∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着网购的日益盛行,物流行业已逐渐成为运输业的主力,已知某大型物流公司有A、B两种型号的货车,A型货车的满载量是B型货车满载量的2倍多4吨,在两车满载的情况下,用A型货车载1400吨货物与用B型货车载560吨货物的用车数量相同.
(1)1辆A型货车和1辆B型货车的满载量分别是多少?
(2)该物流公司现有120吨货物,可以选择上述两种货车运送,在满载的情况下,有几种方案可以一次性运完?
查看答案和解析>>
科目:初中数学 来源: 题型:
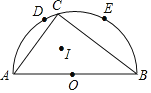
【题目】如图,已知点D,E是半圆O上的三等分点,C是弧DE上的一个动点,连结AC和BC,点I是△ABC的内心,若⊙O的半径为3,当点C从点D运动到点E时,点I随之运动形成的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生到商场参加社会实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如表所示:

(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解本校学生平均每天的体育活动时间情况,随机抽取部分学生进行问卷调查,并将调查结果人数分为A,B,C,D四个等级设活动时间为t(小时),A:t<1,B:1≤t<1.5,C:1.5≤t<2,D:t≥2,根据调查结果绘制了如图所示的两幅不完整的统计图.
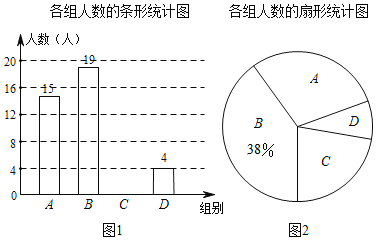
请你根据图中信息解答下列问题:
(1)该校共调查了多少名学生;
(2)将条形统计图补充完整;
(3)求出表示A等级的扇形圆心角的度数;
(4)在此次问卷调查中,甲班有2人平均每天大课间活动时间不足1小时,乙班有3人平均每天大课间活动时间不足1小时,若从这5人中任选2人去参加座谈,试用列表或画树状图的方法求选出的2人来自不同班级的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com