
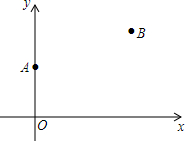 在一条公路的同侧有两个村庄A,B,若在公路上建一个加油站P,使得加油站到两个村庄的距离之和最小,即PA+PB最小.设公路为x轴,A点的坐标为(0,3),B点的坐标为(6,5).
在一条公路的同侧有两个村庄A,B,若在公路上建一个加油站P,使得加油站到两个村庄的距离之和最小,即PA+PB最小.设公路为x轴,A点的坐标为(0,3),B点的坐标为(6,5).分析 (1)先求出点A关于x轴的对称点A′的坐标,连接A′B交x轴于P,此时PA+PB最小,过点B作BC⊥OA,在直角三角形BCA′中利用勾股定理求出A′B的长即可;
(2)用待定系数法求出直线A′B的解析式,然后求出直线与x轴的交点即可.
解答 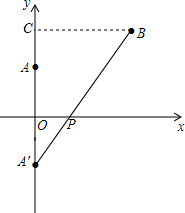 解:作A关于x轴的对称点A′,
解:作A关于x轴的对称点A′,
连接A′B交x轴于P,
则点P就是使得加油站到两个村庄的距离之和最小,即PA+PB最小的点,
A′B的长度即为PA+PB的最小值,
过点B作BC⊥OA,
∵点B(6,5),
∴CO=5,BC=6,
∴CA′=8,
∴A′B=$\sqrt{{6}^{2}+{8}^{2}}$=10;
即PA+PB的最小值=10;
(2)∵A(0,3),
∴点A关于x轴的对称点A′的坐标为(0,-3),
∵A′(0,-3),B(6,5),
设直线A′B的解析式为y=kx+b(k≠0),
∴$\left\{\begin{array}{l}{5=6k+b}\\{-3=b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=-3}\end{array}\right.$.
∴直线A′B的解析式为y=$\frac{4}{3}$x-3,
当y=0时,x=$\frac{9}{4}$
∴P($\frac{9}{4}$,0).
点评 本题考查的是轴对称-最短路线问题以及勾股定理的运用,熟知“两点之间线段最短”是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 利用一面长22米的墙围成一个形状为长方形的养鸡场.如图所示,养鸡场的一面靠墙其他三面用竹篱笆围成,并在一侧留有1米宽的门.现有长度为54米的竹篱笆.大李计划围成的养鸡场的长比宽多7米.小李计划围成的养鸡场的长比宽多4米,请你通过计算分析,谁的方案能够实现?此时养鸡场的面积是多少?
利用一面长22米的墙围成一个形状为长方形的养鸡场.如图所示,养鸡场的一面靠墙其他三面用竹篱笆围成,并在一侧留有1米宽的门.现有长度为54米的竹篱笆.大李计划围成的养鸡场的长比宽多7米.小李计划围成的养鸡场的长比宽多4米,请你通过计算分析,谁的方案能够实现?此时养鸡场的面积是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
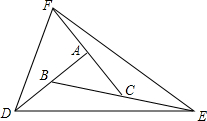 如图,△ABC的面积是10,将AB、BC、CA分别延长一倍到D、E、F,两两连接D、E、F,得到一个新的△DEF.则△DEF的面积为( )
如图,△ABC的面积是10,将AB、BC、CA分别延长一倍到D、E、F,两两连接D、E、F,得到一个新的△DEF.则△DEF的面积为( )| A. | 50 | B. | 60 | C. | 70 | D. | 80 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com