
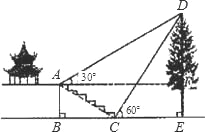
【题目】如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1: ![]() ,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题一定成立的是 ( )
①对顶角相等; ②同位角相等,两直线平行;③全等三角形的周长相等;④面积相等的两个三角形全等
A. ①②③ B. ①④ C. ②④ D. ②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站台乙下车,最后步行到学校(在整个过程中小丽步行的速度不变),图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.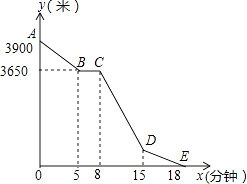
(1)求小丽步行的速度及学校与公交站台乙之间的距离;
(2)当8≤x≤15时,求y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列条件中,不能证明△ABC≌△DCB的是( )
A.AB=CD,AC=BD
B.AB=CD,∠ABC=∠BCD
C.∠ABC=∠DCB,∠A=∠D
D.AB=CD,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将多项式﹣5a2bc+3ab2﹣abc各项提公因式后,另一个因式是( )
A.5ac﹣3ab+c
B.5bc﹣3b+c
C.﹣5ac+3b+c
D.﹣5bc+3b+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由;
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com