
分析 (1)根据相邻两个偶数的平方差,可得答案;
(2)根据相邻两个偶数的平方差,神秘数的定义,可得答案;
(3)根据相邻两个奇数的平方差,神秘数的定义,可得答案.
解答 解:(1)设(2k+2)2-(2k)2=52,解得k=6,
52是神秘数;
(2k+2)2-(2k)2=2015,
解得k=$\frac{2011}{8}$,
2015不是神秘数;
(2)两个连续的偶数为2k和2k+2(其中k为非负数),由这两个连续偶数构造的“神秘数”是4的倍数,
理由如下:
(2k+2)2-(2k)2=8k+4=4(2k+1),
两个连续的偶数为2k和2k+2(其中k为非负数),由这两个连续偶数构造的“神秘数”是4的倍数;
(3)两个连续奇数的平方差(k取正数)不是“神秘数”,理由如下:
(2k+1)2-(2k-1)2=8k,又神秘数为4的倍数,而不是8的倍数;
故两个连续奇数的平方差(k取正数)不是“神秘数”.
点评 本题考查了平方差公式,利用平方差公式是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由$\frac{x}{5}$=20得x=4 | B. | 由3x-2=2x+2得x=4 | ||
| C. | 由2x-3=3x得x=3 | D. | 由3x-5=7得3x=7-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
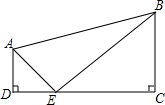 如图,在四边形ABCD中,AD∥BC,∠C=∠D=90°,AD=2,BC=3,CD=7,若点E是边DC上的一个动点,当DE为何值时,△EAD与△EBC相似?
如图,在四边形ABCD中,AD∥BC,∠C=∠D=90°,AD=2,BC=3,CD=7,若点E是边DC上的一个动点,当DE为何值时,△EAD与△EBC相似?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com