
����Ŀ��ij���ξ�����Ʊ�۸�涨���£�
ijУ���꼶��֯�ס��������92��ȥ�þ������棬���мװ����������Ұ������Ҽװ���������90�ˣ�����������������Ʊ��һ��Ӧ��7760Ԫ��
��1������ס�����������������������Ʊ����ô�ȸ��Թ�����Ʊ���Խ�ʡ����Ǯ��
��2���ס�����������ж���ѧ����
��3������װ���10��ѧ����ѧУ�������ܲμ�������Σ�������Ϊ��������Ƴ�������Ʊ�ķ�������ָ����ʡǮ�ķ�����
���𰸡�
��1���⣺����ס���������������������Ʊ��70��92=6440��Ԫ����
�ȸ��Թ�����Ʊ�����Խ�ʡ��7760��6440=1320��Ԫ��
��2���⣺��װ���ѧ��x�ˣ�������46��x��90�������Ұ���ѧ����92��x���ˣ�
������ã�80x+90����92��x��=7760��
��ã�x=52��
��92��52=40���ˣ���
�ʼװ���52�ˣ��Ұ���40��
��3���⣺����һ�����Թ�����Ʊ��42��90+40��90=6860��Ԫ����
�����������Ϲ�����Ʊ�裨42+40����80=6560��Ԫ����
�����������Ϲ���91����Ʊ��91��70=6370��Ԫ����
��6860��6560��6370��
��Ӧ�ü���������������ѡ��70Ԫһ�ι���91����Ʊ��ʡǮ
����������1���ȼ���ס���������������������Ʊ��Ҫ�ķ��ã����ø��Թ�����Ʊ�ķ���-�ס���������������������Ʊ��Ҫ�ķ��ü��ɣ���2�������������������Ʊ��һ��Ӧ��7760Ԫ���з�����⣻��3����������Թ�����Ʊ��Ҫ�ķ��ã����Ϲ�����Ʊ��Ҫ�ķ��ã����Ϲ���91����Ʊ��Ҫ�ķ��ã��ٱȽϴ�С�����ҳ���ʡǮ�ķ�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڱ���2008���29����˻�ǰϦ��ij�����������з��֣����˻Ἢ��� �����ޡ�ƽ��ÿ����۳�20�ף�ÿ��ӯ��40Ԫ��Ϊ��ӭ�Ӱ��˻ᣬ�̳�������ȡ�ʵ��Ľ��۴�ʩ������������������ӯ����������ٿ�档���г����鷢�֣����ÿ����4Ԫ����ôƽ��ÿ��Ϳɶ��۳�8�ס�Ҫ��ƽ��ÿ�������ۼ�������ӯ��1200Ԫ����ôÿ��Ӧ���۶��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��1��Լ��������Ϊһ���µ�������ţ��ȹ۲����и�ʽ��
1��3=1��4+3=7��3������1��=3��4��1=11��5�� ![]() =5��4+
=5��4+ ![]() =
= ![]() ��
��
5��4=5��4+4=24��4������3��=4��4��3=13������ ![]() ����0=����
����0=���� ![]() ����4+0=��
����4+0=�� ![]()
��
�������ϵ��������д��a��b= ��
��2�����ݣ�1����Լ����a��b����������������ٺ͢�
������x��3����x��ֵ����13����x��ֵ��
����2m��n=2������㣺��m��n������2m+n����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ԭ���������y=��x2��2mx��m��1����x�����һ������ΪA������P����1��m����ֱ��PD��x���ڵ�D�����������ڵ�B��BC��x�ύ�������ڵ�C��

��1����m=2ʱ��
�����߶�BC�ij���ֱ��AB����Ӧ�ĺ�����ϵʽ��
��������Q��ֱ��AB�Ϸ������������˶������Q�ںδ�ʱ����QAB��������
������F���������ϣ���PF=PC����ֱ��д�����������ĵ�F�����ꣻ
��2����m��1ʱ������CA��CP����mΪ��ֵʱ��CA��CP��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���������� ![]() ����ƽ��ֱ������ϵ�У�����
����ƽ��ֱ������ϵ�У����� ![]() ����
���� ![]() ���ϣ�������߾���������ƽ��.ֱ��
���ϣ�������߾���������ƽ��.ֱ�� ![]() ��
�� ![]() ��ĸ�������ÿ��1����λ���ٶ�ƽ�ƣ���ƽ�ƵĹ����У���ֱ�߱�������
��ĸ�������ÿ��1����λ���ٶ�ƽ�ƣ���ƽ�ƵĹ����У���ֱ�߱������� ![]() �ı����صõ��߶γ�Ϊ
�ı����صõ��߶γ�Ϊ ![]() ��ƽ�Ƶ�ʱ��Ϊ
��ƽ�Ƶ�ʱ��Ϊ ![]() ���룩��
���룩�� ![]() ��
�� ![]() �ĺ���ͼ����ͼ2��ʾ����ͼ1�еĵ�
�ĺ���ͼ����ͼ2��ʾ����ͼ1�еĵ� ![]() ������Ϊ �� ͼ2��
������Ϊ �� ͼ2�� ![]() ��ֵΪ.
��ֵΪ.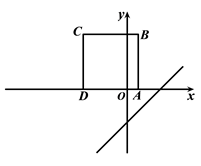

ͼ1 ͼ2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D��˫�����ϣ�AD��ֱ![]() �ᣬ����Ϊ
�ᣬ����Ϊ
A����C��AD�ϣ�CBƽ����![]() �ύ˫�����ڵ�B��ֱ��AB��
�ύ˫�����ڵ�B��ֱ��AB��![]() �ύ�ڵ�F����֪AC��
�ύ�ڵ�F����֪AC��
AD=1��3����C��������2��2����
��1�����˫���ߵĽ���ʽ��
��2������OFA�������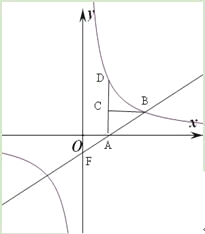
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͬѧ��,���������о���![]() ������������,�õ��������������ε������ı���ʽΪ12+22+32+��+n2.��nΪ100ʱ,Ӧ��μ��������εľ��������?�������Ǿ�һ����̽��������������.����,ͨ��̽�������Ѿ�֪��:
������������,�õ��������������ε������ı���ʽΪ12+22+32+��+n2.��nΪ100ʱ,Ӧ��μ��������εľ��������?�������Ǿ�һ����̽��������������.����,ͨ��̽�������Ѿ�֪��: ![]() ��
��![]() ʱ,���ǿ���������:
ʱ,���ǿ���������:
(1)�۲첢����:
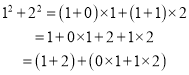 ;
;
![]()
=![]()
=![]() ;
;
![]()
=![]()
=![]() ( );��
( );��
(2)���ɽ��ۣ�
![]() ��
��![]() ��
��![]()
=![]() ��
��![]()
=( )+[ ]
= +
=![]() .
.
(3)ʵ��Ӧ��:
ͨ������̽������,���ǾͿ��������nΪ100ʱ,�����������������ε��ܸ����� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
��1����ͼ�٣���AOB=60�㣬ODƽ�֡�BOC��OEƽ�֡�AOC�����EOD=�ȣ�
��2������AOB=90�㣬�����������䣬���EOD=;
��3������AOB=���������������䣬���EOD= ��
��4�����Ӧ�ã���ͼ�ڣ���֪�߶�AB��C���߶�AB����һ�㣬D��E�ֱ���AC��CB���е㣬�Բ���DE��AB��������ϵΪ �� ��д�������̣�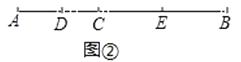
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com