
ЁОЬтФПЁПШчЭМЫљЪОЃЌЭјИёжНжаЕФУПИіаЁЗНИёЖМЪЧБпГЄЮЊ1ЕФе§ЗНаЮЃЌЮвУЧАбвдИёЕуМфСЌЯпЮЊБпЕФШ§НЧаЮГЦЮЊЁАИёЕуШ§НЧаЮЁБЃЌЭМжаЕФ![]() ЪЧИёЕуШ§НЧаЮЃЎдкНЈСЂЦНУцжБНЧзјБъЯЕКѓЃЌЕу
ЪЧИёЕуШ§НЧаЮЃЎдкНЈСЂЦНУцжБНЧзјБъЯЕКѓЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉАб![]() ЯђЯТЦНвЦ5ИёКѓЕУЕН
ЯђЯТЦНвЦ5ИёКѓЕУЕН![]() ЃЌаДГіЕу
ЃЌаДГіЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФзјБъЃЌВЂЛГі
ЕФзјБъЃЌВЂЛГі![]() ЃЛ
ЃЛ
ЃЈ2ЃЉАб![]() ШЦЕу
ШЦЕу![]() АДЫГЪБеыЗНЯђа§зЊ
АДЫГЪБеыЗНЯђа§зЊ![]() КѓЕУЕН
КѓЕУЕН![]() ЃЌаДГіЕу
ЃЌаДГіЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФзјБъЃЌВЂЛГі
ЕФзјБъЃЌВЂЛГі![]() ЃЛ
ЃЛ
ЃЈ3ЃЉАб![]() вдЕу
вдЕу![]() ЮЊЮЛЫЦжааФЗХДѓЕУЕН
ЮЊЮЛЫЦжааФЗХДѓЕУЕН![]() ЃЌЪЙЗХДѓЧАКѓЖдгІЯпЖЮЕФБШЮЊ
ЃЌЪЙЗХДѓЧАКѓЖдгІЯпЖЮЕФБШЮЊ![]() ЃЌаДГіЕу
ЃЌаДГіЕу![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФзјБъЃЌВЂЛГі
ЕФзјБъЃЌВЂЛГі![]() ЃЎ
ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЭММћНтЮіЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉЭММћНтЮіЃЌ
ЃЛЃЈ2ЃЉЭММћНтЮіЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЛЃЈ3ЃЉЭММћНтЮіЃЌ
ЃЛЃЈ3ЃЉЭММћНтЮіЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Лђ
Лђ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉжБНгРћгУЦНвЦЕФаджЪЕУГіЖдгІЕуЮЛжУНјЖјЕУГіД№АИЃЛ
ЃЈ2ЃЉжБНгРћгУа§зЊЕФаджЪЕУГіЖдгІЕуЮЛжУНјЖјЕУГіД№АИЃЛ
ЃЈ3ЃЉжБНгРћгУЮЛЫЦЭМаЮЕФаджЪЕУГіЖдгІЕуЮЛжУНјЖјЕУГіД№АИЃЎ
ЃЈ1ЃЉШчЭМЫљЪОЃЌЁїA1B1C1МДЮЊЫљЧѓЃК
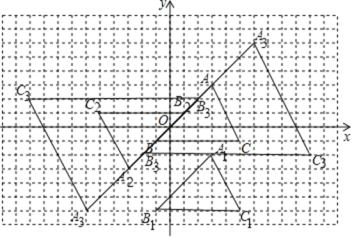
ЕуA1ЃЌB1ЃЌC1ЕФзјБъЗжБ№ЮЊЃЈ3ЃЌ-2ЃЉЃЌЃЈ-1ЃЌ-6ЃЉЃЌЃЈ5ЃЌ-6ЃЉ
ЃЈ2ЃЉШчЭМЫљЪОЁїA2B2C2МДЮЊЫљЧѓЃК
ЕуA2ЃЌB2ЃЌC2ЕФзјБъЗжБ№ЮЊЃЈ-3ЃЌ-3ЃЉЃЌЃЈ1ЃЌ1ЃЉЃЌЃЈ-5ЃЌ1ЃЉЃЛ
ЃЈ3ЃЉШчЭМЫљЪОЁїA3B3C3МДЮЊЫљЧѓЃК
ЕуA3ЃЌB3ЃЌC3ЕФзјБъЗжБ№ЮЊЃЈ6ЃЌ6ЃЉЃЌЃЈ-2ЃЌ-2ЃЉЃЌЃЈ10ЃЌ-2ЃЉЛђЃЈ-6ЃЌ-6ЃЉЃЌЃЈ2ЃЌ2ЃЉЃЌЃЈ-10ЃЌ2ЃЉЃЎ


 ПЦбЇЪЕбщЛюЖЏВсЯЕСаД№АИ
ПЦбЇЪЕбщЛюЖЏВсЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
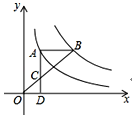
ЁОЬтФПЁПШчЭМЃЌЕуAдкЫЋЧњЯпyЃН![]() ЩЯЃЌЕуBдкЫЋЧњЯпyЃН
ЩЯЃЌЕуBдкЫЋЧњЯпyЃН![]() ЃЈkЁй0ЃЉЩЯЃЌABЁЮxжсЃЌЙ§ЕуAзїADЁЭxжсгкDЃЎСЌНгOBЃЌгыADЯрНЛгкЕуCЃЌШєACЃН2CDЃЌдђkЃН__ЃЎ
ЃЈkЁй0ЃЉЩЯЃЌABЁЮxжсЃЌЙ§ЕуAзїADЁЭxжсгкDЃЎСЌНгOBЃЌгыADЯрНЛгкЕуCЃЌШєACЃН2CDЃЌдђkЃН__ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЃЈ
ЃЈ![]() ЃЉЕФЭМЯѓгыЗДБШР§КЏЪ§
ЃЉЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкЕкЖўЁЂЫФЯѓЯоФкЕФAЁЂBСНЕуЃЌгыyжсНЛгкCЕуЃЌЙ§ЕуAзїAHЁЭyжсЃЌДЙзуЮЊHЃЌOH=3ЃЌtanЁЯAOH=
ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкЕкЖўЁЂЫФЯѓЯоФкЕФAЁЂBСНЕуЃЌгыyжсНЛгкCЕуЃЌЙ§ЕуAзїAHЁЭyжсЃЌДЙзуЮЊHЃЌOH=3ЃЌtanЁЯAOH=![]() ЃЌЕуBЕФзјБъЮЊЃЈmЃЌЉ2ЃЉЃЎЧѓЃК
ЃЌЕуBЕФзјБъЮЊЃЈmЃЌЉ2ЃЉЃЎЧѓЃК
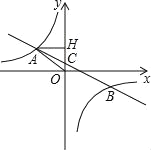
ЃЈ1ЃЉЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉаДГіЕБЗДБШР§КЏЪ§ЕФжЕДѓгквЛДЮКЏЪ§ЕФжЕЪБ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() , Еу
, Еу![]() ЪЧБп
ЪЧБп![]() ЩЯвЛЖЏЕу(ВЛгы
ЩЯвЛЖЏЕу(ВЛгы![]() жиКЯ)ЃЌ
жиКЯ)ЃЌ![]() =
=![]()
![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ,Чв
,Чв![]() ,дђЯпЖЮ
,дђЯпЖЮ![]() ЕФзюДѓжЕЮЊ___ЃЎ
ЕФзюДѓжЕЮЊ___ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУХфЗНЗЈНтЯТСаЗНГЬЪБЃЌХфЗНгаДэЮѓЕФЪЧЃЈ ЃЉ
A.![]() ЛЏЮЊ
ЛЏЮЊ![]() B.
B.![]() ЛЏЮЊ
ЛЏЮЊ![]()
C.![]() ЛЏЮЊ
ЛЏЮЊ![]() D.
D.![]() ЛЏЮЊ
ЛЏЮЊ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
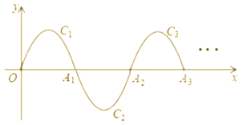
ЁОЬтФПЁПШчЭМЃЌвЛЖЮХзЮяЯпЃК![]()
![]() МЧЮЊ
МЧЮЊ![]() ЃЌЫќгы
ЃЌЫќгы![]() жсНЛгкСНЕу
жсНЛгкСНЕу![]() ЃЌ
ЃЌ![]() ЃЛНЋ
ЃЛНЋ![]() ШЦ
ШЦ![]() а§зЊ
а§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЌНЛ
ЃЌНЛ![]() жсгк
жсгк![]() ЃЛНЋ
ЃЛНЋ![]() ШЦ
ШЦ![]() а§зЊ
а§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЌНЛ
ЃЌНЛ![]() жсгк
жсгк![]() ЃЛ
ЃЛ![]() ШчДЫНјааЯТШЅЃЌжБжСЕУЕН
ШчДЫНјааЯТШЅЃЌжБжСЕУЕН![]() ЃЌШєЕу
ЃЌШєЕу![]() дкЕк
дкЕк![]() ЖЮХзЮяЯп
ЖЮХзЮяЯп![]() ЩЯЃЌдђ
ЩЯЃЌдђ![]() ___________ЃЎ
___________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ЕФЭМЯѓгы
ЕФЭМЯѓгы![]() жсНЛгк
жсНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() ЕФзѓБпЃЉ
ЕФзѓБпЃЉ![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊХзЮяЯпЕФЖЅЕуЃЎ
ЮЊХзЮяЯпЕФЖЅЕуЃЎ
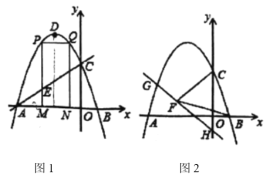
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЕуЃЈЕу
ЩЯвЛЕуЃЈЕу![]() ВЛгыЕу
ВЛгыЕу![]() ЁЂ
ЁЂ![]() жиКЯЃЉЃЌЙ§Еу
жиКЯЃЉЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЃЌгыжБЯп
жсЕФДЙЯпЃЌгыжБЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌгыХзЮяЯпНЛгкЕу
ЃЌгыХзЮяЯпНЛгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() НЛХзЮяЯпгкЕу
НЛХзЮяЯпгкЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсгкЕу
жсгкЕу![]() ЃЌПЩЕУОиаЮ
ЃЌПЩЕУОиаЮ![]() ЃЌШчЭМ1ЃЌЕу
ЃЌШчЭМ1ЃЌЕу![]() дкЕу
дкЕу![]() зѓБпЃЌЕБОиаЮ
зѓБпЃЌЕБОиаЮ![]() ЕФжмГЄзюДѓЪБЃЌЧѓ
ЕФжмГЄзюДѓЪБЃЌЧѓ![]() ЕФжЕЃЌВЂЧѓГіДЫЪБЕФ
ЕФжЕЃЌВЂЧѓГіДЫЪБЕФ![]() ЕФУцЛ§ЃЛ
ЕФУцЛ§ЃЛ
ЃЈ3ЃЉвбжЊ![]() ЃЌЕу
ЃЌЕу![]() дкХзЮяЯпЩЯЃЌСЌ
дкХзЮяЯпЩЯЃЌСЌ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌШє
ЃЌШє![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
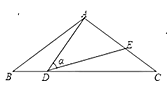
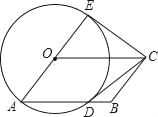
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮOABCЪЧЦНааЫФБпаЮЃЌвдOЮЊдВаФЃЌOAЮЊАыОЖЕФдВНЛABгкЕуDЃЌбгГЄAOНЛЁбOгкЕуEЃЌСЌНгCDЁЂCEЃЌШєCEЪЧЁбOЕФЧаЯпЃЎ
ЃЈ1ЃЉЧѓжЄЃКCDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєЁбOЕФАыОЖЮЊ4ЃЌOCЃН7ЃЌЧѓBDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇЮЊСЫЖдаТбаЗЂЕФвЛжжВњЦЗНјааКЯРэЖЈМлЃЌНЋИУВњЦЗАДФтЖЈЕФМлИёНјааЪдЯњЃЌЭЈЙ§Жд5ЬьЕФЪдЯњЧщПіНјааЭГМЦ,ЕУЕНШчЯТЪ§ОнЃК

ЃЈ1ЃЉЭЈЙ§ЖдЩЯУцБэИёжаЕФЪ§ОнНјааЗжЮіЃЌЗЂЯжЯњСПyЃЈМўЃЉгыЕЅМл![]() ЃЈдЊ/МўЃЉжЎМфДцдквЛДЮКЏЪ§ЙиЯЕЃЌЧѓyЙигк
ЃЈдЊ/МўЃЉжЎМфДцдквЛДЮКЏЪ§ЙиЯЕЃЌЧѓyЙигк![]() ЕФКЏЪ§ЙиЯЕЪНЃЈВЛашвЊаДГіКЏЪ§здБфСПЕФШЁжЕЗЖЮЇЃЉЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЈВЛашвЊаДГіКЏЪ§здБфСПЕФШЁжЕЗЖЮЇЃЉЃЛ
ЃЈ2ЃЉдЄМЦдкНёКѓЕФЯњЪлжаЃЌЯњСПгыЕЅМлШдШЛДцдкЃЈ2ЃЉжаЕФЙиЯЕЃЌЧвИУВњЦЗЕФГЩБОЪЧ20дЊ/Мў.ЮЊЪЙЙЄГЇЛёЕУзюДѓРћШѓЃЌИУВњЦЗЕФЕЅМлгІЖЈЮЊЖрЩй?
ЃЈ3ЃЉЮЊБЃжЄВњЦЗдкЪЕМЪЪдЯњжаЯњЪлСПВЛЕУЕЭгк30МўЃЌЧвЙЄГЇЛёЕУЕУРћШѓВЛЕУЕЭгк400дЊЃЌЧыжБНгаДГіЕЅМл![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com