
【题目】如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.

(1)说明BE=CF的理由;
(2)如果AB=5,AC=3,求AE、BE的长.
【答案】(1)见解析;(2)AE=4,BE=1.
【解析】
(1)连接DB,DC,证明Rt△BED≌Rt△CFD,再运用全等三角形的性质即可证明;
(2).先证明△AED≌△AFD得到AE=AF,设BE=x,则CF=x, 利用线段的和差即可完成解答.
(1)证明:连接BD,CD,

∵ AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠BED=∠CFD=90°,
∵DG⊥BC且平分BC,
∴BD=CD,
在Rt△BED与Rt△CFD中,
![]() ,
,
∴Rt△BED≌Rt△CFD(HL),
∴BE=CF;
(2)解:在△AED和△AFD中,

∴△AED≌△AFD(AAS),
∴AE=AF,
设BE=x,则CF=x,
∵AB=5,AC=3,AE=AB﹣BE,AF=AC+CF,
∴5﹣x=3+x,解得:x=1,
∴BE=1,即AE=AB﹣BE=5﹣1=4.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点P是BC边上一动点(不与点B、C重合),连接AP,作射线PD,使∠APD=60°,PD交AC于点D,已知AB=a,设CD=y,BP=x,则y与x函数关系的大致图象是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点N沿路线O→A→C运动.

(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△ONC的面积是△OAC面积的![]() 时,求出这时点N的坐标.
时,求出这时点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是反比例函数y=![]() (x>0)图象上一点,直线y=kx+b过点A并且与两坐标轴分别交于点B,C,过点A作AD⊥x轴,垂足为D,连接DC,若△BOC的面积是4,则△DOC的面积是______.
(x>0)图象上一点,直线y=kx+b过点A并且与两坐标轴分别交于点B,C,过点A作AD⊥x轴,垂足为D,连接DC,若△BOC的面积是4,则△DOC的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() 、
、![]() .
.
⑴如图①,若![]() ,求
,求![]() 的度数;
的度数;
⑵如图②,若![]() ,求
,求![]() 的度数;
的度数;
⑶若![]()
![]() ,直接写出用
,直接写出用![]() 表示
表示![]() 大小的代数式.
大小的代数式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“首届中国西部(银川)房车生活文化节”期间,某汽车经销商推出A、B、C、D四种型号的小轿车共1000辆进行展销.C型号轿车销售的成交率为50%,其它型号轿车的销售情况绘制在图1和图2两幅尚不完整的统计图中.
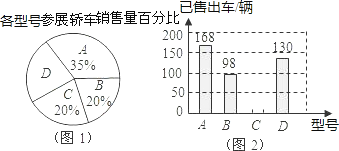
(1)参加展销的D型号轿车有多少辆?
(2)请你将图2的统计图补充完整;
(3)通过计算说明,哪一种型号的轿车销售情况最好?
(4)若对已售出轿车进行抽奖,现将已售出A、B、C、D四种型号轿车的发票(一车一票)放到一起,从中随机抽取一张,求抽到A型号轿车发票的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF,AD+EC=AB.
(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
(4)请你猜想:当∠A为多少度时,∠EDF+∠EFD=120°,并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:△ABE≌△CAD;
(2)求∠BPQ的度数;
(3)求AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com