
【题目】如图1,已知抛物线![]() 与x轴从左至右交于A,B两点,与y轴交于点c.
与x轴从左至右交于A,B两点,与y轴交于点c.

(1)若抛物线过点T(1,-![]() ),求抛物线的解析式;
),求抛物线的解析式;
(2)在第二象限内的抛物线上是否存在点D,使得以A、B、D三点为顶点的三角形与△ABC相似?若存在,求a的值;若不存在,请说明理由.
(3)如图2,在(1)的条件下,点P的坐标为(-1,1),点Q(6,t)是抛物线上的点,在x轴上,从左至右有M、N两点,且MN=2,问MN在x轴上移动到何处时,四边形PQNM的周长最小?请直接写出符合条件的点M的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)M(-
;(3)M(-![]() ,0)
,0)
【解析】
(1)把T的坐标代入解析式,求出a的值,写出解析式;
(2)根据点D在第二象限,∠DAB为钝角,所以当A、B、D三点为顶点的三角形与△ABC相似时,只能∠DAB与∠ACB对应,所以分以下两种情况讨论:①如图2,当△BDA∽△ABC时,∠BAC=∠ABD,
②当△DBA∽△ABC时,如图3,∠ABC=∠ABD,分别列比例式,得方程求解;
(3)本题介绍两种解法:
解法一:先求出Q的坐标为(6,10),通过轴对称作出使四边形PQNM的周长最小时的M、N的位置,因为PQ、NM为定值,要想周长最小,则需要PM+NQ最小,即想办法做到一直线上,因此作P关于x轴的对称点P′,找到P′G=2,且P′G∥x轴,利用平移构建平行四边形P′GNM,从而得到x轴上的M和N,求出M的坐标.
解法二:同理得Q的坐标,作P关于x轴的对称点P′,过Q作QH∥x轴,交y轴于H,在QH上从Q起取一点Q',使QQ'=2,连接Q'P',交x轴于一点,则此点为M,根据P'Q'的解析式可得M的坐标.
(1)如图1,把T(1,﹣![]() )代入抛物线y=
)代入抛物线y=![]() (x﹣2)(x+a)得:
(x﹣2)(x+a)得:
﹣![]() =
=![]() (1﹣2)(1+a),
(1﹣2)(1+a),
解得:a=4,
∴抛物线的解析式为:y=![]() x2+
x2+![]() x﹣2;
x﹣2;
(2)当x=0时,y=![]() ×(﹣2)×a=﹣2,
×(﹣2)×a=﹣2,
∴C(0,﹣2),
当y=0时,![]() (x﹣2)(x+a)=0,
(x﹣2)(x+a)=0,
x1=2,x2=﹣a,
∴A(﹣a,0)、B(2,0),
如图2,过D作DE⊥x轴于E,
设D(m,n),
∵点D在第二象限,∠DAB为钝角,
∴分两种情况:
①如图2,当△BDA∽△ABC时,∠BAC=∠ABD,
∴tan∠BAC=tan∠ABD,即![]() ,
,
∴![]() ,
,
n=![]() ,
,
则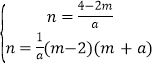 ,
,
解得:m=﹣2﹣a或2,
∴E(﹣2﹣a,0),
由勾股定理得:AC=![]() ,
,
∵![]() ,
,
∴![]() ,
,
BD=![]() ,
,
∵△BDA∽△ABC,
∴![]() ,
,
∴AB2=ACBD,
即(a+2)2=![]() ,
,
解得:0=16,此方程无解;
②当△DBA∽△ABC时,如图3,∠ABC=∠ABD,
∵B(2,0),C(0,﹣2),
∴OB=OC=2,
∴△OBC是等腰直角三角形,
有BC=2![]() ,
,
∴∠OCB=∠OBC=45°,
∴∠ABC=∠ABD=45°,
∴DE=BE,
n=﹣m+2,
∴BD=![]() ,
,
∵△DBA∽△ABC,
∴![]() ,
,
∴AB2=BDBC,
∴(a+2)2=![]() 2
2![]() =4n,
=4n,
则 ,
,
解得: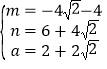 ,
,
则a=2+2![]() ;
;
(3)解法一:当x=6时,y=![]() (6﹣2)(6+4)=10,
(6﹣2)(6+4)=10,
∴Q(6,10),
如图4,作P关于x轴的对称点P′,过P′作P′G∥x轴,且P′G=2,连接GQ交x轴于N,过P′作P′M∥GN,交x轴于M,
此时,QG就是MP+NQ的最小值,由于PQ、NM为定值,所以此时,四边形PMNQ的周长最小,
∵P(﹣1,1),
∴P′(﹣1,﹣1),
∵P′G∥MN,P′M∥GN,
∴四边形P′GNM是平行四边形,
∴MN=P′G=2,NG=P′M=PM,
∴G(1,﹣1),
设GQ的解析式为:y=kx+b,
把G(1,﹣1)和Q(6,10)代入得:![]() ,
,
解得: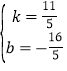 ,
,
∴GQ的解析式为:y= 当y=0时,x= ∴N( ∵MN=2, ∴M(﹣ 解法二:如图5,同理得Q(6,10), P(﹣1,1)关于x轴的对称点P′(﹣1,﹣1),过Q作QH∥x轴,交y轴于H,在QH上从Q起取一点Q',使QQ'=2,连接Q'P',交x轴于一点,则此点为M,此时,四边形PMNQ的周长最小, ∵Q'(4,10),P′(﹣1,﹣1), 易得P'Q'的解析式为:y= 当y=0时, ∴M(﹣![]() x﹣
x﹣![]() ,
,![]() ,
,![]() ,0),
,0),![]() ,0).
,0).![]() x+
x+![]() ,
,![]() x+
x+![]() =0,x=﹣
=0,x=﹣![]() ,
,![]() ,0).
,0).


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
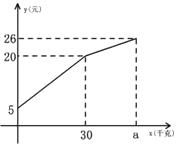
【题目】一农民带上若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的土豆千克数与他手中持有的钱数(含备用零钱)的关系,如图所示,结合图象回答下列问题.
(1)农民自带的零钱是多少?
(2)试求降价前y与x之间的关系式
(3)由表达式你能求出降价前每千克的土豆价格是多少?
(4)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,试问他一共带了多少千克土豆?
查看答案和解析>>
科目:初中数学 来源: 题型:
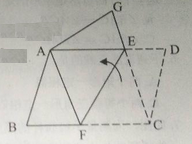
【题目】如图,将一张平行四边形纸片ABCD沿着线段EF折叠(点E、F分别在AB边和BC边上),使得点C落在点A处,点D落在点G出。
(1)如果连接EC,那么线段GE与EC在同一条直线上吗?为什么?
(2)试判断四边形AFCE的形状,并说明你是怎样判断的?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①abc>0;②2a+b>0;③b2﹣4ac>0;④a﹣b+c>0,其中正确的个数是( )
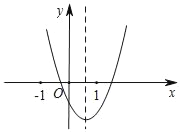
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线C1:y1=mx2﹣4mx+2n﹣1与平行于x轴的直线交于A、B两点,且A点坐标为(﹣1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,﹣1);③m>![]() ;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是
;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是![]() ≤a<2;⑤不等式mx2﹣4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( )
≤a<2;⑤不等式mx2﹣4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( )
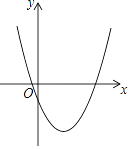
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:(一)如果我们能找到两个实数x、y使![]() 且
且![]() ,这样
,这样![]() ,那么我们就称
,那么我们就称![]() 为“和谐二次根式”,则上述过程就称之为化简“和谐二次根式”.
为“和谐二次根式”,则上述过程就称之为化简“和谐二次根式”.
例如:![]() .
.
(二)在进行二次根式的化简与运算时,我们有时还会碰上如![]() 一样的式子,其实我们还可以将其进一步化简:
一样的式子,其实我们还可以将其进一步化简: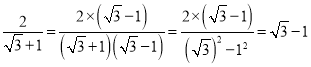 ,那么我们称这个过程为分式的分母有理化.
,那么我们称这个过程为分式的分母有理化.
根据阅读材料解决下列问题:
(1)化简“和谐二次根式”:①![]() ___________,②___________;
___________,②___________;
(2)已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)设![]() 的小数部分为
的小数部分为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象经过点
的图象经过点![]() .
.
(1)若函数图象经过原点,求k,b的值
(2)若点![]() 是该函数图象上的点,当
是该函数图象上的点,当![]() 时,总有
时,总有![]() ,且图象不经过第三象限,求k的取值范围.
,且图象不经过第三象限,求k的取值范围.
(3)点![]() 在函数图象上,若
在函数图象上,若![]() ,求n的取值范围.
,求n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在矩形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 的三个顶点
的三个顶点![]() 、
、![]() 、
、![]() 分别在矩形
分别在矩形![]() 边
边![]() 、
、![]() 、
、![]() 上,
上,![]() .
.
![]() 如图
如图![]() ,当四边形
,当四边形![]() 为正方形时,求
为正方形时,求![]() 的面积;
的面积;
![]() 如图
如图![]() ,当四边形
,当四边形![]() 为菱形时,设
为菱形时,设![]() ,
,![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出函数的定义域.
的函数关系式,并写出函数的定义域.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com