
【题目】如图,在平面直角坐标系中,O为□ABCD的对称中心,点A的坐标为(-2,-2),AB=5,AB//x轴,反比例函数y=![]() 的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C′落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
的图象经过点D,将□ABCD沿y轴向下平移,使点C的对应点C′落在反比例函数的图象上,则平移过程中线段AC扫过的面积为( )
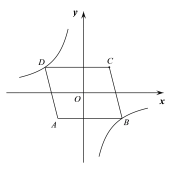
A.10B.18C.20D.24
【答案】C
【解析】
根据O为ABCD的对称中心,AB=5,AB∥x轴交y轴于点E,点A的坐标为(-2,-2),可求点C、B的坐标,进而求出反比例函数的关系式,由平移可求出点C′的坐标,知道平移的距离,即平行四边形的底,再根据点的坐标,可求出平行四边形的高,最后根据面积公式求出结果.
∵AB=5,AB∥x轴交y轴于点E,点A的坐标为(-2,-2),
∴BE=5-2=3,OE=2,
∴B(3,-2)代入反比例函数的关系式得,k=-2×6=-6,
∴反比例函数的解析式为![]() ,
,
∵O为ABCD的对称中心,点A的坐标为(-2,-2),
∴点C的坐标为(2,2),
平移后,如图,
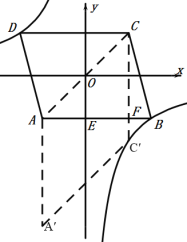
当![]() 时,
时,![]()
∴点C′(2,-3),
∴CC′=2-(-3)=2+3=5,
CC′交AB于F,则AF=AE+EF=2+2=4,
∴平行四边形ACC′A′的面积为5×4=20,
故选:C.


科目:初中数学 来源: 题型:
【题目】甲、乙两地相距![]() 一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是
一列快车和一列慢车都从甲地驶往乙地,慢车先行驶1小时后,快车才开始行驶.已知快车的速度是![]() 以快车开始行驶计时,设时间为
以快车开始行驶计时,设时间为![]() , 两车之间的距离为
, 两车之间的距离为![]() ,图中的折线是
,图中的折线是![]() 与
与![]() 的函数关系的部分图象,根据图象解决以下问题:
的函数关系的部分图象,根据图象解决以下问题:

(1)慢车的速度是_ _![]() ,点
,点![]() 的坐标是_ _;
的坐标是_ _;
(2)线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数关系式是_ ;
之间的函数关系式是_ ;
(3)试在图中补全点![]() 以后的图象.
以后的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线AC,BD相交于点O,AB∶BC=3∶2,过点B作BE∥AC,过点C作CE∥DB,BE,CE交于点E,连接DE,则tan∠EDC等于()
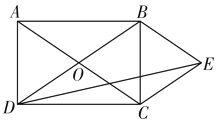
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并解决相应的问题.
巧设密码
在日常生活中,微信支付、取款、上网等都需要密码.有一种用因式分解生成密码的程序,方便记忆.例如:对于多项式![]() ,因式分解的结果是
,因式分解的结果是![]() .若取
.若取![]() ,
,![]() ,则各个因式的值分别是
,则各个因式的值分别是![]() ,
,![]() ,
,![]() ,于是就可以把“
,于是就可以把“![]() ”作为一个六位数的密码
”作为一个六位数的密码
问题解决:
(1)按材料中的原理,若取![]() ,
,![]() ,生成的密码是_______;
,生成的密码是_______;
(2)若将程序修改为:整式![]() 因式分解的结果,取
因式分解的结果,取![]() ,
,![]() 时(来源
时(来源![]() 年
年![]() 月出生),用上述方法产生的密码是多少?(写出一种即可)
月出生),用上述方法产生的密码是多少?(写出一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
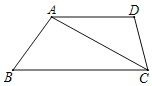
【题目】如图,在四边形ABCD中,AD∥BC.
(1)求作直线EF使得EF交AD于点E,交BC于点F且使得EA=EC,FA=FC(尺规作图,保留作图痕迹,不写作法);
(2)连接AF、CE,判断四边形AFCE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活节奏的加快以及智能手机的普及,外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台,已知某外卖平台的送餐费用与送餐距离有关(该平台只给5千米范围内配送),为调査送餐员的送餐收入,现从该平台随机抽取80名点外卖的用户进行统计,按送餐距离分类统计结果如下表:
送餐距离x(千米) | 0 | 1 | 2 | 3 | 4 |
数量 | 12 | 20 | 24 | 16 | 8 |
(1)从这80名点外卖的用户中任取一名用户,该用户的送餐距离不超过3千米的概率为 ;
(2)以这80名用户送餐距离为样本,同一组数据取该小组数据的中间值(例如第二小组(1<x ≤2)的中间值是1.5),试估计利用该平台点外卖用户的平均送餐距离;
(3)若该外卖平台给送餐员的送餐费用与送餐距离有关,不超过2千米时,每份3元;超过2千米但不超4千米时,每份5元;超过4千米时,每份9元. 以给这80名用户所需送餐费用的平均数为依据,若送餐员一天的目标收入不低于150元,试估计一天至少要送多少份外卖?
查看答案和解析>>
科目:初中数学 来源: 题型:
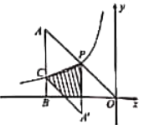
【题目】如图点P为双曲线![]() 上一动点.连接OP并延长到点A,使
上一动点.连接OP并延长到点A,使![]() ,过点A作x轴的垂线,垂足为B,交双曲线于点C.当
,过点A作x轴的垂线,垂足为B,交双曲线于点C.当![]() 时,连接PC,将
时,连接PC,将![]() 沿直线PC进行翻折,则翻折后的
沿直线PC进行翻折,则翻折后的![]() 与四边形BOPC的重叠部分(图中阴影部分)的面积是_______________
与四边形BOPC的重叠部分(图中阴影部分)的面积是_______________
查看答案和解析>>
科目:初中数学 来源: 题型:
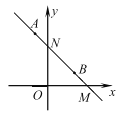
【题目】在平面直角坐标系中,已知点![]() ,
,![]() ,直线
,直线![]() 与
与![]() 轴和
轴和![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,若抛物线
,若抛物线![]() 与直线
与直线![]() 有两个不同的交点,其中一个交点在线段
有两个不同的交点,其中一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),另一个交点在线段
两个端点),另一个交点在线段![]() 上(包含
上(包含![]() ,
,![]() 两个端点),则
两个端点),则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() 或
或![]() C.
C. ![]() D.
D. ![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一边长为![]() 的等边
的等边![]() 游乐场,某人从边
游乐场,某人从边![]() 中点
中点![]() 出发,先由点
出发,先由点![]() 沿平行于
沿平行于![]() 的方向运动到
的方向运动到![]() 边上的点
边上的点![]() ,再由
,再由![]() 沿平行于
沿平行于![]() 方向运动到
方向运动到![]() 边上的点
边上的点![]() ,又由点
,又由点![]() 沿平行于
沿平行于![]() 方向运动到
方向运动到![]() 边上的点
边上的点![]() ,则此人至少要运动_______
,则此人至少要运动_______![]() ,才能回到点
,才能回到点![]() .如果此人从
.如果此人从![]() 边上意一点出发,按照上面的规律运动,则此人至少走______
边上意一点出发,按照上面的规律运动,则此人至少走______![]() ,就能回到起点.
,就能回到起点.
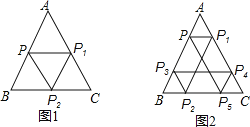
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com