
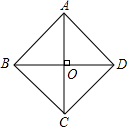
 解:如图,在菱形ABCD中,对角线AC与BD相交于O.则AC⊥BD,则AO=
解:如图,在菱形ABCD中,对角线AC与BD相交于O.则AC⊥BD,则AO=| 1 |
| 2 |
| 1 |
| 2 |
| x2 |
| 25 |
| 1 |
| 2 |
| 1 |
| 2 |
| 24 |
| 25 |
| 24 |
| 25 |


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 在今年第9号超强台风“圣帕”来临之际,B市气象局测得台风中心位于B市正东方向500km的A处,正以20km/h千米的速度向西北方向移动,距台风中心400的范围内受到影响,问B市是否受到这次台风的影响?如果有影响,则持续的时间有多长?
在今年第9号超强台风“圣帕”来临之际,B市气象局测得台风中心位于B市正东方向500km的A处,正以20km/h千米的速度向西北方向移动,距台风中心400的范围内受到影响,问B市是否受到这次台风的影响?如果有影响,则持续的时间有多长?查看答案和解析>>
科目:初中数学 来源: 题型:
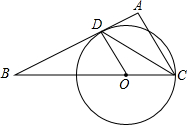 如图,在△ABC中,∠A=90°,CD平分∠ACB交AB于D,AD<AC,过C,D两点作⊙O且圆心O在BC上.若CD=5,△ADC的面积为6,求半径.
如图,在△ABC中,∠A=90°,CD平分∠ACB交AB于D,AD<AC,过C,D两点作⊙O且圆心O在BC上.若CD=5,△ADC的面积为6,求半径.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com