
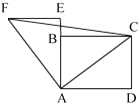
【题目】如图,在矩形ABCD中,AD=4,DC=3,将△ADC按逆时针绕点A旋转到△AEF(A、B、E在同一直线上),连接CF,则CF的长为( )
A. ![]() B. 5 C. 7 D.
B. 5 C. 7 D. ![]()
【答案】A
【解析】
由于△ADC按逆时针方向绕点A旋转到△AEF,显然△ADC≌△AEF,则有∠EAF=∠DAC,AF=AC,那么∠EAF+∠EAC=∠DAC+∠EAC,即∠FAC=∠BAD=90°.在Rt△ACD中,利用勾股定理可求AC,同理在Rt△FAC中,利用勾股定理可求CF.
∵△ADC按逆时针方向绕点A旋转到△AEF,
∴△ADC≌△AEF,
∴∠EAF=∠DAC,AF=AC,
∴∠EAF+∠EAC=∠DAC+∠EAC,
∴∠FAC=∠BAD,
又∵四边形ABCD是矩形,
∴∠BAD=∠ADC=90°,
∴∠FAC=90°,
又∵在Rt△ADC中,AC=![]() ,
,
∴在Rt△FAC中,CF=![]() .
.
故选A.


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接并延长AE交CD于F,连接BD分别交CE、AF于G、H,下列结论:①∠CEH=45;②GF∥DE;③2OH+DH=BD;④BG=![]() DG;⑤
DG;⑤![]() .其中正确的结论是( )
.其中正确的结论是( )
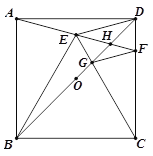
A. ①②③ B. ①②④ C. ①②⑤ D. ②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知:如图,E、F分别是ABCD的AD、BC边上的点,且AE=CF.
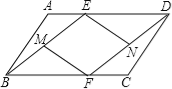
(1)求证:△ABE≌△CDF;
(2)若M、N分别是BE、DF的中点,连接MF、EN,试判断四边形MFNE是怎样的四边形,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
求证:BD是四边形ABCD的“相似对角线”;
(3)如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2![]() ,求FH的长.
,求FH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校20名数学教师的年龄(单位:岁)情况如下:29,42,58,37,53,52,49,24,37,46,42,55,40,38,50,26,54,26,44,52.
(1)填写下面的频率分布表:
分组 | 频数 | 频率 |
19.5~29.5 | ||
29.5~39.5 | ||
39.5~49.5 | ||
49.5~59.5 | ||
合计 |
(2)画出数据的频数分布直方图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD下方一点,将△PCD绕点P顺时针旋转60°后,恰好点D与点A重合,得到△PEA,连接EB,问:△ABE是什么特殊三角形?请说明理由.
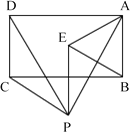
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上.如果BC=4,△ABC的面积是6,那么这个正方形的边长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E为边AD的中点,且∠ABC=60°,AB=6,BE交AC于点F,则AF=( )
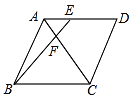
A. 1 B. 2 C. 2.5 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com