如图，在△ABC中，∠A=40°，有一块直角三角板DEF的两条直角边DE、DF分别经过点B、C，若直角顶点D在三角形外部，则∠ABD+∠ACD的度数是__________度．
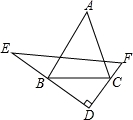
230度．
【考点】多边形内角与外角．
【分析】要求∠ABD+∠ACD的度数，只要求出∠ABC+∠CBD+∠ACB+∠BCD，利用三角形内角和定理得出∠ABC+∠ACB=180°﹣∠A=180°﹣40°=140°；根据三角形内角和定理，∠CBD+∠BCD=∠E+∠F=90°，∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+90°=230°．
【解答】解：在△ABC中，∠A+∠ABC+∠ACB=180°，∠A=40°
∴∠ABC+∠ACB=180°﹣40°=140°
在△BCD中，∠D+∠BCD+∠CBD=180°
∴∠BCD+∠CBD=180°﹣∠D
在△DEF中，∠D+∠E+∠F=180°
∴∠E+∠F=180°﹣∠D
∴∠CBD+∠BCD=∠E+∠F=90°
∴∠ABD+∠ACD=∠ABC+∠CBD+∠ACB+∠BCD=140°+90°=230°．
故答案为：230．
【点评】考查三角形内角和定理，外角性质．熟练掌握这些性质是解题的关键．
科目：初中数学 来源： 题型：
如图，在6×10的正方形网格中，每个小正方形的边长均为1，每个小正方形顶点叫做格点，△ABC的三个顶点
和点D、E、F、G、H、K均在格点上，现以D、E、F、G、H、K中的三个点为顶点画三角形．
（1）在图①中画出一个三角形与△ABC全等；
（2）在图②中画出一个三角形与△ABC面积相等但不全等．
查看答案和解析>>
科目：初中数学 来源： 题型：
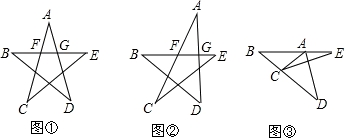
探究：中华人民共和国国旗上的五角星的每个角均相等，小明为了计算每个角的度数，画出了如图①的五角星，每个角均相等，并写出了如下不完整的计算过程，请你将过程补充完整．
解：∵∠AFG=∠C+∠E，∠AGF=∠B+∠D．
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D．
∵∠A+∠AFG+∠AGF=__________°，
∴∠A+∠B+∠C+∠D+∠E=__________°，
∴∠A=∠B=∠C=∠D=∠E=__________°．
拓展：如图②，小明改变了这个五角星的五个角的度数，使它们均不相等，请你帮助小明求∠A、∠B、∠C、∠D、∠E的和．
应用：如图③．小明将图②中的点A落在BE上，点
C落在BD上，若∠B=∠D=36°，则∠CAD+∠ACE+∠E=__________°．
查看答案和解析>>
科目：初中数学 来源： 题型：
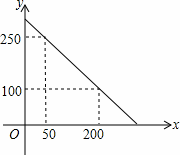
某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒，乙品牌的进货单价是甲品牌进货单价的2倍，考虑各种因素，预计购进乙品牌文具盒的数量y（个）与甲品牌文具盒的数量x（个）之间的函数关系如图所示．当购进的甲、乙品牌的文具盒中，甲有120个时，购进甲、乙品牌文具盒共需72
00元．
（1）根据图象
，求y与x之间的函数关系式；
（2）求甲、乙两种品牌的文具盒进货单价；
（3）若该超市每销售1个甲种品牌的文具盒可获利4元，每销售1个乙种品牌的文具盒可获利9元，根据学生需求，超市老板决定，准备用不超过6300元购进甲、乙两种品牌的文具盒，且这两种品牌的文具盒全部售出后获利不低于1795元，问该超市有几种进货方案？哪种
方案能使获利最大？最大获利为多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，
，且
，则