
【题目】已知顶点为A(2,﹣1)的抛物线与y轴交于点B,与x轴交于C、D两点,点C坐标(1,0);
(1)求这条抛物线的表达式;
(2)连接AB、BD、DA,求![]() 的大小;
的大小;
(3)点P在x轴正半轴上位于点D的右侧,如果∠APB=45°,求点P的坐标.
【答案】(1)y=x2﹣4x+3 (2)![]() (3)点P(3+
(3)点P(3+![]() ,0).
,0).
【解析】(1)设抛物线的解析式为y=a(x-2)2-1,将点C的坐标代入可求得a的值,从而可得到抛物线的解析式;
(2)先求得点B、C、D的坐标,由点A、B、D的坐标可得到∠BDO=∠ADO=45°,从而可证明△ABD为直角三角形,然后依据两点间的距离公式可求得AB和BD的长,最后依据余弦定理的定义求解即可;
(3)先证明△ADP∽△PDB,依据相似三角形的性质可得到DP2=BD×AD,从而可求得DP的长,故此可得到点P的坐标.
解:(1)∵顶点为A(2,﹣1)的抛物线经过点C(1,0),

∴可以假设抛物线的解析式为y=a(x﹣2)2﹣1,
把(1,0)代入可得a=1,
∴抛物线的解析式为y=x2﹣4x+3.
(2)令y=0,x2﹣4x+3=0,解得x=1或3,
∴C(1,0),D(3,0),令x=0,y=3,
∴B(0,3)∵OB=OD=3,∴∠BDO=45°,
∵A(2,﹣1),D(3,0),
∴∠ADO=45°,∴∠BDA=90°,∴![]() ·
·
(3)∵∠BDO=∠DPB+∠DBP=45°,∠APB=∠DPB+∠DPA=45°,∴∠DBP=∠APD,
∵∠PDB=∠ADP=135°,∴△PDB∽△ADP,∴PD2=BDAD=3![]() ×
×![]() =6,
=6,
∴PD=![]() ,∴OP=3+
,∴OP=3+![]() ,∴点P(3+
,∴点P(3+![]() ,0).
,0).
“点睛”本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、锐角三角函数的定义、学生三角形的性质和判断,证得△ABD为直角三角形是解答问题(2)的关键;证得△ADP∽△PDB是解答问题(3)的关键.


科目:初中数学 来源: 题型:
【题目】如图,△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交与点P,若∠CAP=50°,则∠BPC的度是( )

A. 80° B. 60° C. 50° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C(﹣2,1),
△ABC绕原点顺时针旋转90°,得到△A1B1C1,△A1B1C1向左平移2个单位,再向下平移5个单
位得到△A2B2C2.
(1)画出△A1B1Cl和△A2B2C2;
(2)P(a,b)是△ABC的AC边上一点,△ABC经旋转、平移后点P的对应点分别为P1、P2,请
写出点P1、P2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个正比例函数图象与一个一次函数图象交于点A(3,4),且一次函数的图象与y轴相交于点B(0,-5).

(1)求这两个函数的表达式;
(2)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国南海海域面积约为3500000 km2 , 用科学记数法表示正确的是( )
A.3.5×105 km2
B.3.5×106 km2
C.3.5×107 km2
D.3.5×108 km2
查看答案和解析>>
科目:初中数学 来源: 题型:
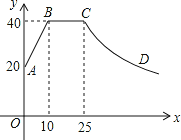
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指数y随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):
(1)求出线段AB,曲线CD的解析式,并写出自变量的取值范围;
(2)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?
(3)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角,墙DF足够长,墙DE长为12米,现用20米长的篱笆围成一个矩形花园ABCD,点C在墙DF上,点A在墙DE上,(篱笆只围AB,BC两边).
(1)如何才能围成矩形花园的面积为75m2?
(2)能够围成面积为101m2的矩形花园吗?如能说明围法,如不能,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com