

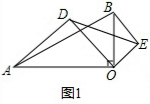
| OA |
| OB |
| OD |
| OE |
| 3 |
| AD |
| BE |
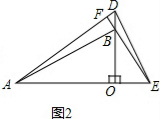
| OA |
| OB |
| 3 |
| OA |
| OB |
| OD |
| OE |
| OA |
| OB |
| 3 |
| OD |
| OE |
| 3 |
| OA |
| OB |
| OD |
| OE |
| AD |
| BE |
| OA |
| OB |
| 3 |
| OA |
| OB |
| OD |
| OE |
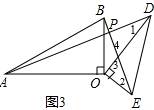

| OA |
| OB |
| OD |
| OE |
| 3 |


科目:初中数学 来源: 题型:
| A、40米 | B、30米 |
| C、60米 | D、100米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在△ABO中,OA=OB边的中点,C是AB的中点,⊙O过点C,且与OA交于点E,与OB交于点F,连接CE、CF,点M在⊙O上,连接EM、FM.
如图,在△ABO中,OA=OB边的中点,C是AB的中点,⊙O过点C,且与OA交于点E,与OB交于点F,连接CE、CF,点M在⊙O上,连接EM、FM.查看答案和解析>>
科目:初中数学 来源: 题型:
| 板房 | A种板材(m2) | B种板材(m2) | 安置人数 |
| 甲型 | 108 | 61 | 12 |
| 乙型 | 156 | 51 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:
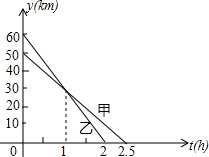 甲、乙两人骑自行车前往A地,他们距A地的路程s(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
甲、乙两人骑自行车前往A地,他们距A地的路程s(km)与行驶时间t(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 为了营造“美好,和谐,健康”的文明社区,某市现有一小区规划设计如图所示,准备建三个小亭子A、B、C,但由于不小心C处的位置被损坏,已经看不清楚了,只记得C处在B处北偏东45°,在A处南偏东60°处,而且C处亭子区域是以C为圆心,半径为10米的圆形.
为了营造“美好,和谐,健康”的文明社区,某市现有一小区规划设计如图所示,准备建三个小亭子A、B、C,但由于不小心C处的位置被损坏,已经看不清楚了,只记得C处在B处北偏东45°,在A处南偏东60°处,而且C处亭子区域是以C为圆心,半径为10米的圆形.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、①⑤ | B、①④ |
| C、①④⑤ | D、②④⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com