
【题目】如图,已知在矩形ABCD中,AB=2,BC=3,P是线段AD上的一动点,连接PC,过点P作PE⊥PC交AB于点E.以CE为直径作⊙O,当点P从点A移动到点D时,对应点O也随之运动,则点O运动的路程长度为_____.

【答案】![]() .
.
【解析】
连接AC,取AC的中点K,连接OK.设AP=x,AE=y,求出AE的最大值,求出OK的最大值,由题意点O的运动路径的长为2OK,由此即可解决问题.
解:连接AC,取AC的中点K,连接OK.设AP=x,AE=y,
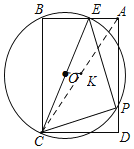
∵PE⊥CP
∴∠APE+∠CPD=90°,且∠AEP+∠APE=90°
∴∠AEP=∠CPD,且∠EAP=∠CDP=90°
∵△APE∽△DCP
∴![]() ,
,
即x(3﹣x)=2y,
∴y=![]() x(3﹣x)=﹣
x(3﹣x)=﹣![]() x2+
x2+![]() x=﹣GXdjs4436236(x﹣
x=﹣GXdjs4436236(x﹣![]() )2+
)2+![]() ,
,
∴当x=![]() 时,y的最大值为
时,y的最大值为![]() ,
,
∴AE的最大值=![]() ,
,
∵AK=KC,EO=OC,
∴OK=![]() AE=
AE=![]() ,
,
∴OK的最大值为![]() ,
,
由题意点O的运动路径的长为2OK=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作等腰三角形外接圆”的尺规作图过程.
已知:如图1,在![]() 中,AB=AC.
中,AB=AC.
求作:等腰![]() 的外接圆.
的外接圆.

作法:
①如图2,作![]() 的平分线交BC于D ;
的平分线交BC于D ;
②作线段AB的垂直平分线EF;
③EF与AD交于点O;
④以点O为圆心,以OB为半径作圆.
所以,![]() 就是所求作的等腰
就是所求作的等腰![]() 的外接圆.
的外接圆.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留痕迹);
(2)完成下面的证明.
![]() AB=AC,
AB=AC,![]() ,
,
![]() _________________________.
_________________________.
![]() AB的垂直平分线EF与AD交于点O,
AB的垂直平分线EF与AD交于点O,
![]() OA=OB,OB=OC
OA=OB,OB=OC
(填写理由:______________________________________)
![]() OA=OB=OC.
OA=OB=OC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等
(1)若从中只录用一人,恰好选到思政专业毕业生的概率是 :
(2)若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
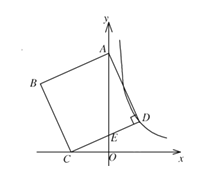
【题目】如图,在平面直角坐标系中,正方形ABCD的面积为20,顶点A在y轴上,顶点C在x轴上,顶点D在双曲线![]() 的图象上,边CD交y轴于点E,若
的图象上,边CD交y轴于点E,若![]() ,则k的值为______.
,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
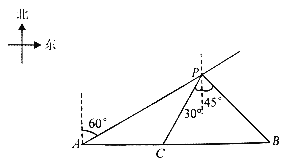
【题目】近日,国产航母山东舰成为了新晋网红,作为我国本世纪建造的第一艘真正意义上的国产航母,承载了我们太多期盼,促使我国在伟大复兴路上加速前行如图,山东舰在一次测试中,巡航到海岛A北偏东60°方向P处,发现在海岛A正东方向有一可疑船只B正沿BA方向行驶。山东舰经测量得出:可疑船只在P处南偏东45°方向,距P处![]() 海里。山东舰立即从P沿南偏西30°方向驶出,刚好在C处成功拦截可疑船只。求被拦截时,可疑船只距海岛A还有多少海里?(
海里。山东舰立即从P沿南偏西30°方向驶出,刚好在C处成功拦截可疑船只。求被拦截时,可疑船只距海岛A还有多少海里?(![]() ,结果精确到0.1海里)
,结果精确到0.1海里)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),某数学活动小组经探究发现:在⊙O中,直径AB与弦CD相交于点P,此时PA· PB=PC·PD
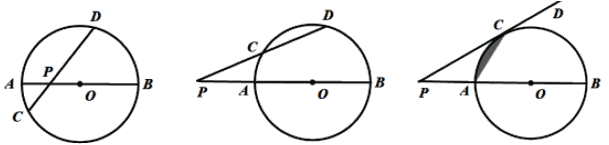
(1)如图(2),若AB与CD相交于圆外一点P, 上面的结论是否成立?请说明理由.
(2)如图(3),将PD绕点P逆时针旋转至与⊙O相切于点C, 直接写出PA、PB、PC之间的数量关系.
(3)如图(3),直接利用(2)的结论,求当 PC= ![]() ,PA=1时,阴影部分的面积.
,PA=1时,阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,已知AB=AC,∠BAC=90°,E为边AC上一点,连接BE.
(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;
(2)如图2,D为AB上一点,且满足AE=AD,过点A作AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M,求证:BG=AF+FG.
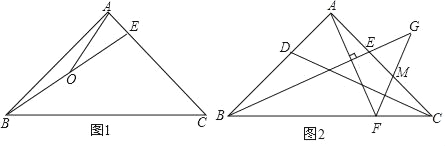
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与边CD相切于点D,点B在⊙O上,连接OB.
(1)求证:DE=OE;
(2)若CD∥AB,求证:BC是⊙O的切线;
(3)在(2)的条件下,求证:四边形ABCD是菱形.
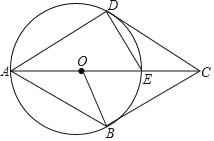
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com