
【题目】如图1,已知a∥b,点A、B在直线a上,点C、D在直线b上,且AD⊥BC于E.
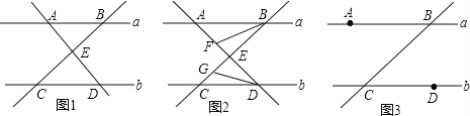
(1)求证:∠ABC+∠ADC=90°;
(2)如图2,BF平分∠ABC交AD于点F,DG平分∠ADC交BC于点G,求∠AFB+∠CGD的度数;
(3)如图3,P为线段AB上一点,I为线段BC上一点,连接PI,N为∠IPB的角平分线上一点,且∠NCD=![]() ∠BCN,则∠CIP、∠IPN、∠CNP之间的数量关系是______.
∠BCN,则∠CIP、∠IPN、∠CNP之间的数量关系是______.
【答案】(1)见解析;(2)225°;(3)3∠CNP=∠CIP+∠IPN或3∠IPN=∠CIP+∠CNP.
【解析】
(1)如图1中,过E作EF∥a,利用平行线的性质即可解决问题;
(2)如图2中,作FM∥a,GN∥b,设∠ABF=∠EBF=x,∠ADG=∠CDG=y,可得x+y=45°,证明∠AFB=180°-(2y+x),∠CGD=180°-(2x+y),推出∠AFB+∠CGD=360°-(3x+3y)即可解决问题;
(3)分两种情形:①当点N在∠DCB内部时,②当点N′在直线CD的下方时,分别画出图形求解即可.
(1)证明:如图1中,过E作EF∥a.
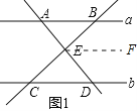
∵a∥b,
∴a∥b∥EF,
∵AD⊥BC,
∴∠BED=90°,
∵EF∥a,
∴∠ABE=∠BEF,
∵EF∥b,
∴∠ADC=∠DEF,
∴∠ABC+∠ADC=∠BED=90°.
(2)解:如图2中,作FM∥a,GN∥b,
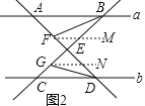
设∠ABF=∠EBF=x,∠ADG=∠CDG=y,
由(1)知:2x+2y=90°,x+y=45°,
∵FM∥a∥b,
∴∠BFD=2y+x,
∴∠AFB=180°-(2y+x),
同理:∠CGD=180°-(2x+y),
∴∠AFB+∠CGD=360°-(3x+3y),
=360°-3×45°=225°.
(3)解:如图,设PN交CD于E.
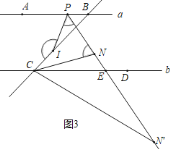
当点N在∠DCB内部时,∵∠CIP=∠PBC+∠IPB,
∴∠CIP+∠IPN=∠PBC+∠BPN+2∠IPE,
∵PN平分∠EPB,
∴∠EPB=∠EPI,
∵AB∥CD,
∴∠NPE=∠CEN,∠ABC=∠BCE,
∵∠NCE=![]() ∠BCN,
∠BCN,
∴∠CIP+∠IPN=3∠PEC+3∠NCE=3(∠NCE+∠NEC)=3∠CNP.
当点N′在直线CD的下方时,同理可知:∠CIP+∠CNP=3∠IPN,
综上所述:3∠CNP=∠CIP+∠IPN或3∠IPN=∠CIP+∠CNP.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,O为AC中点,过点O作AC的垂线分别交AD、BC于点E、F,连接AF、CE.
(1)求证:四边形AFCE是菱形;
(2)若AC=8,EF=6,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
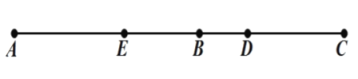
【题目】如图,![]() 为线段
为线段![]() 上靠近点
上靠近点![]() 的三等分点,
的三等分点,![]() 为线段
为线段![]() 上的两点,且满足
上的两点,且满足![]() .
.
(1)若![]() ,求线段
,求线段![]() 的长.
的长.
(2)若图中所有线段的长度之和是线段![]() 长度的
长度的![]() 倍,求
倍,求![]() 的值.
的值.
(3)若![]() ,动点
,动点![]() 从
从![]() 点、动点
点、动点![]() 从
从![]() 点同时出发,分别以
点同时出发,分别以![]() 的速度沿直线
的速度沿直线![]() 向右运动,是否存在某个时刻使得
向右运动,是否存在某个时刻使得![]() 成立?若存在,求此时
成立?若存在,求此时![]() 的长度;若不存在,说明理由.
的长度;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
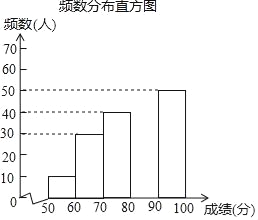
【题目】中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
频数频率分布表
成绩x(分) | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
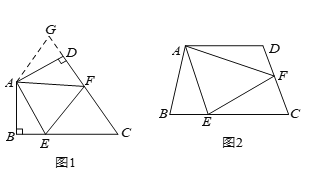
【题目】如图(![]() ),在四边形
),在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() .探究图中线段
.探究图中线段![]() ,
,![]() ,
,![]() 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长![]() 到点
到点![]() ,使
,使![]() ,连接
,连接![]() ,先证明
,先证明![]() ≌
≌![]() ,再证明
,再证明![]() ≌
≌![]() ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.
如图(![]() ),若在四边形
),若在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点,且
上的点,且![]() ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,O为直线AB上一点,过点O作射线OC,![]() ,将一直角三角板
,将一直角三角板![]() 的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
的直角顶点放在点O处,一边ON在射线OA上,另一边OM与OC都在直线AB的上方.
![]() 将图1中的三角板绕点O以每秒
将图1中的三角板绕点O以每秒![]() 的速度沿逆时针方向旋转一周
的速度沿逆时针方向旋转一周![]() 如图2,经过t秒后,ON落在OC边上,则
如图2,经过t秒后,ON落在OC边上,则![]() ______秒
______秒![]() 直接写结果
直接写结果![]() .
.
![]() 如图2,三角板继续绕点O以每秒
如图2,三角板继续绕点O以每秒![]() 的速度沿逆时针方向旋转到起点OA上
的速度沿逆时针方向旋转到起点OA上![]() 同时射线OC也绕O点以每秒
同时射线OC也绕O点以每秒![]() 的速度沿逆时针方向旋转一周,
的速度沿逆时针方向旋转一周,
![]() 当OC转动9秒时,求
当OC转动9秒时,求![]() 的度数.
的度数.
![]() 运动多少秒时,
运动多少秒时,![]() ?请说明理由.
?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于A(﹣3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.

(1)求D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠BAC的平分线与BC的垂直平分线PQ相交于点P,PM⊥AC,PN⊥AB,垂足分别为M、N,AB=5,AC=11,则CM的长度为( )
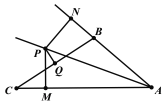
A. 4B. 3C. 2D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com