
����Ŀ����֪��һ�����ǰ壨ֱ�����ǰ�OAB��ֱ�����ǰ�OCD����AOB=90�㣬��ABO=45�㣬��CDO=90�㣬��COD=60�㣩
��1����ͼ1�ڷţ���O��A��C��һֱ���ϣ����BOD�Ķ����Ƕ��٣�
��2����ͼ2����ֱ�����ǰ�OCD�Ƶ�O��ʱ�뷽��ת������ҪOBǡ��ƽ�֡�COD�����AOC�Ķ����Ƕ��٣�
��3����ͼ3�������ǰ�OCD�ڷ��ڡ�AOB�ڲ�ʱ��������OMƽ�֡�AOC������ONƽ�֡�BOD��������ǰ�OCD�ڡ�AOB���Ƶ�O����ת������MON�Ķ����Ƿ����仯��������䣬����ֵ������仯��˵�����ɣ�

���𰸡���1��30�㣻(2) 60�㣻(3) ����75��
��������
�������ǰ�ǵ������ͽ�ƽ���ߵĶ�����
��1��������ǵĶ��弴�ɵõ����ۣ�
��2���ɽ�ƽ���ߵĶ���õ���BOC=![]() ��COD=
��COD=![]() ��60��=30����������ǵĶ��弴�ɵõ����ۣ�
��60��=30����������ǵĶ��弴�ɵõ����ۣ�
��3�����ݽ�ƽ���ߵĶ���õ�![]() ����BOD+��AOC��=
����BOD+��AOC��=![]() ��30��=15����Ȼ����ݽǵĺͲ�ɵõ������
��30��=15����Ȼ����ݽǵĺͲ�ɵõ������
�⣺��1��![]() ��
��
��2����BOC=![]() ��COD=
��COD=![]() ��60��=30�㣬
��60��=30�㣬
���AOC=��AOB����BOC=90�㩁30��=60�㣻
��3����BOD+��AOC=90�㩁��COD=90�㩁60��=30�㣬
![]() ����BOD+��AOC��=
����BOD+��AOC��=![]() ��30��=15�㣬
��30��=15�㣬
��MON=![]() ����BOD+��AOC��+��COD=15��+60��=75��
����BOD+��AOC��+��COD=15��+60��=75��
����MON�Ķ������ᷢ���仯������75�㣮


 ���ſ����ϵ�д�
���ſ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������45����30������ֱ�����dzߵ�ֱ�Ƕ���C������һ��
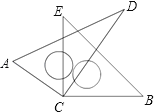
��1������DCE��25�������ACB��______������ACB��150�������DCE��______��
��2�������ACB���DCE�Ĵ�С�к������ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�У���A=30������ͬһƽ���ڣ��ԶԽ���BDΪ�ױ�������Ϊ120���ĵ���������BDE������EBC�Ķ���Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����10������Rt��ABC�У���BAC=![]() ,D��BC���е㣬E��AD���е�������A��AF��BC��BE���ӳ����ڵ�F��
,D��BC���е㣬E��AD���е�������A��AF��BC��BE���ӳ����ڵ�F��

��1����֤����AEF����DEB��
��2��֤���ı���ADCF�����Σ�
��3����AC=4��AB=5��������ADCFD �������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90�㣬AC=BC��б��AB=2��O��AB���е㣬��OΪԲ�ģ��߶�OC�ij�Ϊ�뾶��Բ�Ľ�Ϊ90��������OEF����EF������C����ͼ����Ӱ���ֵ����Ϊ________.
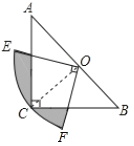
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
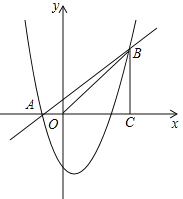
����Ŀ����ͼ����֪������![]() ����A��-1,0����B��4,5�����㣬����B��BC��x�ᣬ����ΪC.
����A��-1,0����B��4,5�����㣬����B��BC��x�ᣬ����ΪC.
��1���������ߵĽ���ʽ��
��2����tan��ABO��ֵ��
��3����M���������ϵ�һ���㣬ֱ��MNƽ����y�ύֱ��AB��N�������M��N��B��CΪ������ı�����ƽ���ı��Σ������M�ĺ�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ž��õĿ��ٷ�չ����������Խ��Խ�ܵ����ǵĹ�ע��ijУѧ����Ϊ�˽���ܼ��š���������֪ʶ���ռ��������������˲���ѧ������������Ϊ���dz��˽⡱�����˽⡱�����˽���١��������˽⡱���࣬������������Ƴ���������ͳ��ͼ��
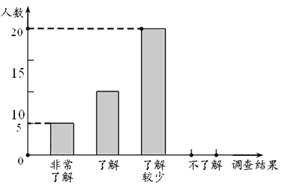

�� ���ε����ѧ�������� ���ˣ����˽���١���ѧ��������ռ�İٷֱ�Ϊ�� ����
�� ��ȫ����ͳ��ͼ��
�� ����У����1300��ѧ���������ͳ�ƽ�������У�����˽⡱��ѧ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��1����![]() Ϊ���������Σ�
����������![]() ��
��![]() ���ǵױ�
���ǵױ�![]() �ϵ�һ�����㣬
�ϵ�һ�����㣬![]() ��
��![]() .
.
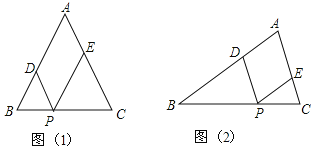
��1����![]() ��ʾ�ı���
��ʾ�ı���![]() ���ܳ�Ϊ������
���ܳ�Ϊ������
��2����![]() �˶���ʲôλ��ʱ���ı���
�˶���ʲôλ��ʱ���ı���![]() �����Σ���˵�����ɣ�
�����Σ���˵�����ɣ�
��3�����![]() ���ǵ���������ͼ��2���������������䣬��
���ǵ���������ͼ��2���������������䣬��![]() �˶���ʲôλ��ʱ���ı���
�˶���ʲôλ��ʱ���ı���![]() �����Σ�����˵�����ɣ�.
�����Σ�����˵�����ɣ�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������˾������960���²�Ʒ��Ҫ���ӹ������Ͷ���г������мס���������������ӹ�������Ʒ,��֪�׳������ӹ�������Ʒ���ҹ��������ӹ���������Ʒ����20��,������ÿ��ӹ����������ҹ���ÿ��ӹ�������![]() ���ס�����������ÿ����ܼӹ����ٸ��²�Ʒ?
���ס�����������ÿ����ܼӹ����ٸ��²�Ʒ?
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com