
【题目】西宁市教育局自实施新课程改革后,学生的自主学习、合作交流能力有很大提高.张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下不完整的统计图,请你根据统计图解答下列问题:
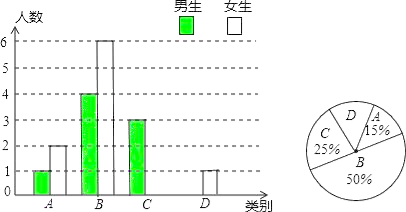
(1)本次调查中,张老师一共调查了 名同学;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,张老师想从被调查的A类和D类学生分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法列出所有等可能的结果,并求出所选两位同学恰好是一位男同学和一位女同学的概率.
【答案】(1)20(2)见解析(3)![]()
【解析】
(1)根据A组总人数与所占的百分比进行计算即可得解;
(2)求出C组的总人数,然后减去男生人数即可得到女生人数,求出D组人数所占的百分比,再求出D组的总人数,然后减去女生人数得到男生人数,最后补全统计图即可;
(3)画出树状图,根据概率公式求解即可.
(1)(1+2)÷15%=20人;
(2)C组人数为:20×25%=5人,
所以,女生人数为5﹣3=2人,
D组人数为:20×(1﹣15%﹣50%﹣25%)=20×10%=2人,
所以,男生人数为2﹣1=1人,
补全统计图如图;
(3)画树状图如图:
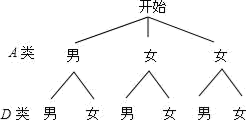
所有等可能结果:男男、男女、女男、女女、女男、女女,
P(一男一女)![]() .
.


科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:
①4ac<b2;
②a>b>c;
③一次函数y=ax+c的图象不经第四象限;
④m(am+b)+b<a(m是任意实数);
⑤3b+2c>0.
其中正确的个数是( )
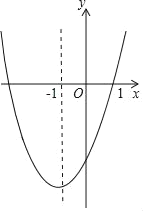
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
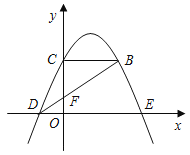
【题目】如图,抛物线y=﹣![]() (x﹣k)2+
(x﹣k)2+![]() 经过点D(﹣1,0),与x轴正半轴交于点E,与y轴交于点C,过点C作CB∥x轴交抛物线于点B.连接BD交y轴于点F.
经过点D(﹣1,0),与x轴正半轴交于点E,与y轴交于点C,过点C作CB∥x轴交抛物线于点B.连接BD交y轴于点F.
(1)求点E的坐标.
(2)求△CFB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
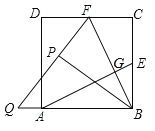
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA的延长线于点Q,则下列结论:
①AE=BF;②S四边形ECFG=S△ABG;③△BFQ是等腰三角形;④![]() .
.
其中一定正确的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
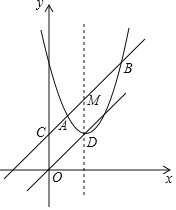
【题目】如图,直线y=x+2与抛物线y=x2﹣2mx+m2+m交于A、B两点(A在B的左侧),与y轴交于点C,抛物线的顶点为D,抛物线的对称轴与直线AB交于点M.
(1)当四边形CODM是菱形时,求点D的坐标;
(2)若点P为直线OD上一动点,求△APB的面积;
(3)作点B关于直线MD的对称点B',以点M为圆心,MD为半径作⊙M,点Q是⊙M上一动点,求QB'+![]() QB的最小值.
QB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,抛物线的对称轴与直线
,抛物线的对称轴与直线![]() 交于点
交于点![]() .
.
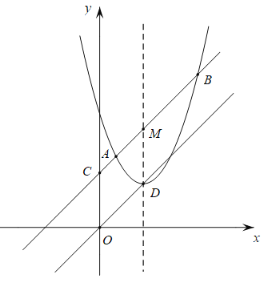
(1)当四边形![]() 是菱形时,求点
是菱形时,求点![]() 的坐标;
的坐标;
(2)若点![]() 为直线
为直线![]() 上一动点,求
上一动点,求![]() 的面积;
的面积;
(3)作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,点
,点![]() 是
是![]() 上一动点,求
上一动点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
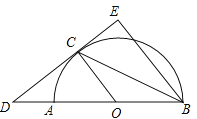
【题目】如图,已知AB是⊙O的直径,CD与⊙O相切于C,BE∥CO.
(1)求证:BC是∠ABE的平分线;
(2)若DC=8,⊙O的半径OA=6,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长都是1个单位长度,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2).

(1)画出△OAB向下平移3个单位长度后的△O1A1B1;
(2)画出△OAB绕点O逆时针旋转90°后的△OA2B2;
(3)在(2)的条件下,求点B旋转到点B2所经过的路径长(结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
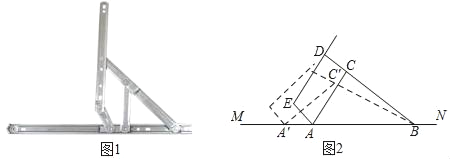
【题目】“滑块铰链”是一种用于连接窗扇和窗框,使窗户能够开启和关闭的连杆式活动链接装置(如图1).图2是“滑块铰链”的平面示意图,滑轨MN安装在窗框上,悬臂DE安装在窗扇上,支点B、C、D始终在一条直线上,已知托臂AC=20厘米,托臂BD=40厘米,支点C,D之间的距离是10厘米,张角∠CAB=60°.
(1)求支点D到滑轨MN的距离(精确到1厘米);
(2)将滑块A向左侧移动到A′,(在移动过程中,托臂长度不变,即AC=A′C′,BC=BC′)当张角∠C′A'B=45°时,求滑块A向左侧移动的距离(精确到1厘米).(备用数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,
≈1.73,![]() ≈2.45,
≈2.45,![]() ≈2.65)
≈2.65)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com