
【题目】已知抛物线C:![]() ,直线l:y=kx(k>0),当k=1时,抛物线C与直线l只有一个公共点.
,直线l:y=kx(k>0),当k=1时,抛物线C与直线l只有一个公共点.
(1)求m的值;
(2)若直线l与抛物线C交于不同的两点A,B,直线l与直线l1:y=﹣3x+b交于点P,且![]() ,求b的值;
,求b的值;
(3)在(2)的条件下,设直线l1与y轴交于点Q,问:是否在实数k使S△APQ=S△BPQ?若存在,求k的值,若不存在,说明理由.

【答案】(1)4;(2)8;(3)不存在.
【解析】
试题分析:(1)两图象有一个交点,则对应的方程组有一组解,即△=0,代入计算即可求出m的值;
(2)作出辅助线,得到△OAC∽△OPD,![]() +
+![]() =2,同理
=2,同理![]() +
+![]() =2,AC,BE是x2﹣(k+3)x+4=0两根,即可;
=2,AC,BE是x2﹣(k+3)x+4=0两根,即可;
(3)由S△APQ=S△BPQ得到AC+BE=2PD,建立方程(k+3)2=16即可.
试题解析:(1)当k=1时,抛物线C与直线l只有一个公共点,∴直线l解析式为y=x,∵ ,∴
,∴![]() ,∴
,∴![]() ,∴△=16﹣4m=0,∴m=4;
,∴△=16﹣4m=0,∴m=4;
(2)如图,分别过点A,P,B作y轴的垂线,垂足依次为C,D,E,则△OAC∽△OPD,∴![]() .
.
同理,![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,即
,即![]() .
.
解方程组:![]() ,得x=
,得x=![]() ,即PD=
,即PD=![]() .
.
由方程组![]() 消去y,得
消去y,得![]() .
.
∵AC,BE是以上一元二次方程的两根,∴AC+BE=k+3,AC×BE=4,∴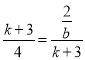 .解得b=8.
.解得b=8.
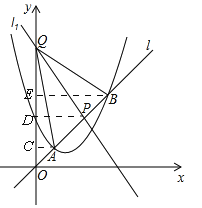
(3)不存在.理由如下:
假设存在,当S△APQ=S△BPQ时,有AP=PB,于是PD﹣AC=PE﹣PD,即AC+BE=2PD.
由(2)可知AC+BE=k+3,PD=![]() ,∴k+3=2×
,∴k+3=2×![]() ,即
,即![]() .
.
解得k=1(舍去k=﹣7).
当k=1时,A,B两点重合,△BQA不存在,∴不存在实数k使S△APQ=S△BPQ.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图:
(1)如果∠1=∠4,根据 , 可得AB∥CD;
(2)如果∠1=∠2,根据 , 可得AB∥CD;
(3)如果∠1+∠3=180,根据 , 可得AB∥CD .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,对称轴为直线x=![]() 的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.
的抛物线经过B(2,0)、C(0,4)两点,抛物线与x轴的另一交点为A.
(1)求抛物线的解析式;
(2)若点P为第一象限内抛物线上的一点,设四边形COBP的面积为S,求S的最大值;
(3)如图2,若M是线段BC上一动点,在x轴是否存在这样的点Q,使△MQC为等腰三角形且△MQB为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级进行法律知识竞赛,共有30道题,答对一道题得4分,不答或答错一道题扣2分.
(1)小红同学参加了竞赛,成绩是90分,请问小红在竞赛中答对了多少道题?
(2)小明也参加了竞赛,考完后他说:“这次竞赛我一定能拿到100分.”请问小明有没有可能拿到100分?试用方程的知识来说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设直线l1和直线l2平行,且l1和l2间的距离为a.如果线段AB在l1的右侧,并设AB关于l1的对称图形是A′B′,而A′B′关于l2的对称图形是A″B″(如图),那么,线段AB和A″B″有什么关系?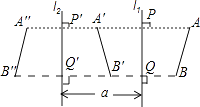
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com