
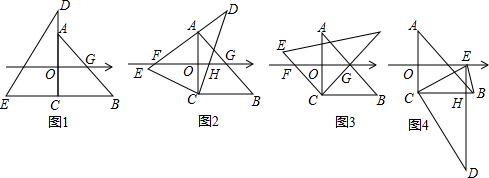
分析 (1)利用等腰直角三角形可得BC的值,易证OG是△ACB的中位线,即可得出点G在数轴上对应的数;
(2)由∠AEC=60°,AC=CE,可得△ACE是等边三角形,由∠DCE=90°,即可得出旋转角θ的角度为30°,利用RT△FOA可得FO的值,即可得出F点在数轴上对应的数;
(3)利用FG∥BC,且FG=BC求得四边形BCFG是平行四边形即可,
(4)①利用RT△COE,可得OC=4,CE=8,可得出∠CEO=30°,进而得出∠CED=60°,由∠OEH=90°,∠COE=∠OCB=90°,即可得出四边形OCHE是矩形;
②在RT△EHB中,求出CH,HB,利用勾股定理BE=$\sqrt{E{H}^{2}+H{B}^{2}}$求解即可.
解答 解:(1)如图1,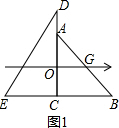
∵RT△ACB是等腰直角三角形,AC=8,
∴BC=8,
∵三角板的直角边AC⊥数轴,AC的中点是数轴原点O,
∴OG=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4,
∴点G在数轴上对应的数是4,
故答案为:4.
(2)如图2,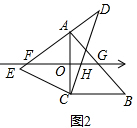
∵∠AEC=60°,AC=CE=8,
∴△ACE是等边三角形,
∵∠DCE=90°,
∴∠ACD=90°-60°=30°,
∴旋转角θ的角度为30°,
∵∠EAC=60°,∠AOF=90°,AO=4,
∴FO=$\sqrt{3}$AO=4$\sqrt{3}$,
(3)如图3,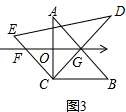
∵点G为AB的中点,
∴∠OCG=45°,
∵∠ECD=90°,
∴∠FCO=45°,
∴FO=CO=4,
∴FG=BG=8,
∵FG∥BC,
∴四边形BCFG是平行四边形,
(4)①如图4,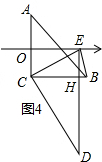
∵在RT△COE中,OC=4,CE=8,
∴∠CEO=30°,
∵∠CED=60°,
∴∠OEH=90°,
∵∠COE=∠OCB=90°,
∴四边形OCHE是矩形;
②∵∠CEO=30°,
∴∠BCE=30°,
∵四边形OCHE是矩形;
∴CH=$\sqrt{3}$EH=4$\sqrt{3}$,
∴HB=BC-CH=8-4$\sqrt{3}$,
∴BE=$\sqrt{E{H}^{2}+H{B}^{2}}$=$\sqrt{{4}^{2}+(8-4\sqrt{3})^{2}}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
点评 本题主要考查了几何变换,涉及特殊直角三角形,矩形的判定与性质,平行四边形的判定及性质及三角形的中位线,解题的关键是灵活的运用特殊直角三角形.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
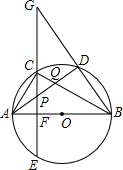 已知:如图,△ABC内接于⊙O,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连结BD并延长交EC的延长线于点G,连结AD,分别交CE、BC于点P、Q.
已知:如图,△ABC内接于⊙O,AB为直径,弦CE⊥AB于F,C是弧AD的中点,连结BD并延长交EC的延长线于点G,连结AD,分别交CE、BC于点P、Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 点P到x轴的距离为3 | B. | 点P到x轴的距离为-3 | ||
| C. | 点P到y轴的距离为4 | D. | 点P到y轴的距离为3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com