
【题目】如图1,点E为矩形ABCD边AD上一点,点P,点Q同时从点B出发,点P沿BE→ED→DC运动到点C停止,点Q沿BC运动到点C停止,它们的运动速度都是1cm/s,设P、Q出发t秒时,△BPQ的面积为y(cm2),已知y与t的函数关系的图象如图2(曲线OM为抛物线的一部分),则下列结论:
①AD=BE=5cm;②当0<t≤5时,y= ![]() t2;③直线NH的解析式为y=﹣
t2;③直线NH的解析式为y=﹣ ![]() t+27;④若△ABE与△QBP相似,则t=
t+27;④若△ABE与△QBP相似,则t= ![]() 秒,
秒,
其中正确结论的个数为( )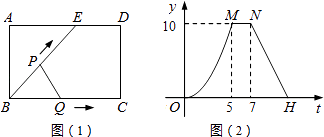
A.4
B.3
C.2
D.1
【答案】B
【解析】解:①根据图(2)可得,当点P到达点E时点Q到达点C,
∵点P、Q的运动的速度都是1cm/s,
∴BC=BE=5cm,
∴AD=BE=5(故①正确);②如图1,过点P作PF⊥BC于点F,
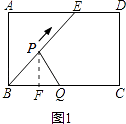
根据面积不变时△BPQ的面积为10,可得AB=4,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB= ![]() =
= ![]() ,
,
∴PF=PBsin∠PBF= ![]() t,
t,
∴当0<t≤5时,y= ![]() BQPF=
BQPF= ![]() t
t ![]() t=
t= ![]() t2(故②正确);③根据5﹣7秒面积不变,可得ED=2,
t2(故②正确);③根据5﹣7秒面积不变,可得ED=2,
当点P运动到点C时,面积变为0,此时点P走过的路程为BE+ED+DC=11,
故点H的坐标为(11,0),
设直线NH的解析式为y=kx+b,
将点H(11,0),点N(7,10)代入可得: ![]() ,
,
解得: 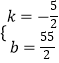 .
.
故直线NH的解析式为:y=﹣ ![]() t+
t+ ![]() ,(故③错误);④当△ABE与△QBP相似时,点P在DC上,如图2所示:
,(故③错误);④当△ABE与△QBP相似时,点P在DC上,如图2所示:
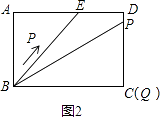
∵tan∠PBQ=tan∠ABE= ![]() ,
,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得:t= ![]() .(故④正确);
.(故④正确);
综上可得①②④正确,共3个.
所以答案是:B.
【考点精析】根据题目的已知条件,利用函数的图象的相关知识可以得到问题的答案,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值.


科目:初中数学 来源: 题型:
【题目】某快递公司针对新客户优惠收费,首件物品的收费标准为:若重量不超过10千克,则免运费;当重量为![]() 千克时,运费为
千克时,运费为![]() 元;第二件物品的收费标准为:当重量为
元;第二件物品的收费标准为:当重量为![]() 千克时,运费为
千克时,运费为![]() 元。
元。
(1)若新客户所奇首件物品的重量为13千克,则运费是多少元?
(2)若新客户所寄首件物品的运费为32元,则物品的重量是多少千克?
(3)若新客户所寄首件物品与第二件物品的重量之比为2:5,共付运费为60元,则两件物品的重量各是多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A,B两地相距4千米,上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲、乙两人离A地的距离(千米)与甲所用的时间(分)之间的关系如图所示.由图中的信息知,乙到达A地的时刻为( )
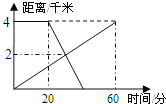
A. 8:30B. 8:35C. 8:40D. 8:45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线y=ax2+bx+3(a<0)与x轴交于A(3,0)、B两点,与y轴交于点C,抛物线的对称轴是直线x=1,D为抛物线的顶点,点E在y轴C点的上方,且CE= ![]() .
.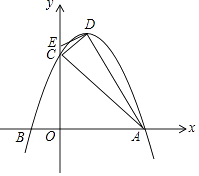
(1)求抛物线的解析式及顶点D的坐标;
(2)求证:直线DE是△ACD外接圆的切线;
(3)在直线AC上方的抛物线上找一点P,使S△ACP= ![]() S△ACD , 求点P的坐标;
S△ACD , 求点P的坐标;
(4)在坐标轴上找一点M,使以点B,C,M为顶点的三角形与△ACD相似,直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )

A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在E处,EQ与BC相交于F.若AD=8cm,AB=6cm,AE=4cm.则△EBF的周长是 cm.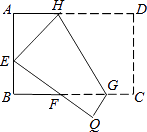
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有小正方形的边长都为1,A、B、C都在格点上.
(1)过点C画直线AB的平行线(不写画法,下同);
(2)过点A画直线BC的垂线,并注明垂足为G;过点A画直线AB的垂线,交BC于点H.
(3)线段_____的长度是点A到直线BC的距离;
(4)线段AG、AH的大小关系为AG_____AH.(填“>”或“<”或“=”),理由________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.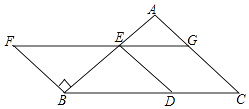
(1)求证:四边形BDEF为平行四边形;
(2)当∠C=45°,BD=2时,求D,F两点间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com