
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图像分別交x轴、y轴于A、B两点.与反比例函数y=﹣ ![]() 的图像交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6.
的图像交于C,D两点,DE⊥x轴于点E.已知DE=3,AE=6. 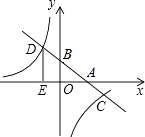
(1)求一次函数的解析式;
(2)直接写出不等式kx+b+ ![]() >0的解集.
>0的解集.
【答案】
(1)解:∵点D在反比例函数y=﹣ ![]() 的图像上,且DE=3,
的图像上,且DE=3,
∴将y=3代入反比例函数解析式得:3=﹣ ![]() ,即x=﹣2,
,即x=﹣2,
点D的坐标为(﹣2,3).
又∵AE=6,
∴A点的坐标为(4,0).
将A与D点的坐标代入一次函数解析式中得: ![]() ,
,
解得: 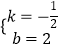 .
.
∴一次函数解析式为y=﹣ ![]() x+2
x+2
(2)解:将y=﹣ ![]() x+2代入y=﹣
x+2代入y=﹣ ![]() 中得:﹣
中得:﹣ ![]() x+2=﹣
x+2=﹣ ![]() ,
,
解得:x1=﹣2,x2=6,
当x=6时,y=﹣ ![]() =﹣1,
=﹣1,
即点C的坐标为(6,﹣1).
kx+b+ ![]() >0可转化为kx+b>﹣
>0可转化为kx+b>﹣ ![]() ,
,
根据两个函数y=﹣ ![]() x+2与y=﹣
x+2与y=﹣ ![]() 的图像可知:
的图像可知:
不等式的解集为:x<﹣2或0<x<6
【解析】(1)根据点D在反比例函数上,且DE=3可得出点D的坐标,再由AE=6可得出点A的坐标,由待定系数法即可求出直线AD的函数解析式;(2)将一次函数解析式代入反比例函数中得处关于x的分式方程,解方程即可得出交点C的坐标,将原不等式进行变形,再结合一次函数与反比例函数图像可直接得出不等式的解集.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置. 
(1)旋转中心是点 , 旋转角度是度;
(2)若连结EF,则△AEF是三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线l:y=﹣ ![]() x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
x+6交y轴于点A,与x轴交于点B,过A、B两点的抛物线m与x轴的另一个交点为C,(C在B的左边),如果BC=5,求抛物线m的解析式,并根据函数图像指出当m的函数值大于0的函数值时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想填空:当黑色瓷砖为28块时,白色瓷砖块数为( )

A. 27 B. 28 C. 33 D. 35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七![]() 班派出
班派出![]() 名同学参加数学竞赛,老师以
名同学参加数学竞赛,老师以![]() 分为基准,把分数超过
分为基准,把分数超过![]() 分的部分记为正数,不足部分记为负数.评分记录如下:
分的部分记为正数,不足部分记为负数.评分记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 这
这![]() 名同学中最高分和最低分各是多少?
名同学中最高分和最低分各是多少?
![]() 超过基准分的和低于基准分的各有多少人?
超过基准分的和低于基准分的各有多少人?
![]() 这十二名同学的平均成绩是多少?
这十二名同学的平均成绩是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
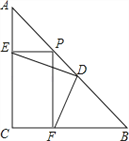
【题目】在△ABC中,∠C=90°,AC=BC=3,D为AB的中点,点P是AB上的一个动点,PE⊥AC于点E,PF⊥BC于点F.
(1)求证:AE=PE;
(2)求证:DE=DF;
(3)连接EF,EF的最小值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)-14-![]() ×[2-(-3)]; (2)(-3)-1
×[2-(-3)]; (2)(-3)-1![]() ×
×![]() -6÷|-
-6÷|-![]() |;
|;
(3)2×[5+![]() ]-(-|-4|÷
]-(-|-4|÷![]() );(4)-
);(4)-![]() -[-3+(-3)÷(-
-[-3+(-3)÷(-![]() )].
)].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com